Kerasと関数型プログラミングを使えば、深層学習(ディープ・ラーニング)は楽ちんですよ
2017/10/25
深層学習(ディープ・ラーニング)ってのは、つまるところ、バックプロパゲーション(逆誤差伝播法)が可能な計算グラフ(計算式)を作って、計算グラフ中のパラメーターに設定すべき値を大量データでキアイで学習させるだけ。しかも、色々と定石が定まってきている(たとえば「畳込みをするならバッチ・ノーマライゼーション→ReLU→畳込みの順にすると精度が上がるよ」とか「分類の場合、畳み込み結果を直接全結合層に入れるより画像全体で平均プーリングした方がパラメーター数が少なくなっていいよ」とか)なので、定石を組み合わせるだけでいろいろできちゃう。ライブラリが計算式をカプセル化してくれますから、計算グラフといっても実際は数式いらずだし。あと、ライブラリが自動でバックプロバゲーション可能な計算グラフを作ってくれるますから、バックプロバゲーションのことも全く考えなくてオッケー。
そして、論文には最新の計算グラフが数式で定義してあるし、大抵はコードも公開されています。だから論文の数式と公開されたコードを読めばすぐに最新の深層学習を適用できる……はずなのですけど、数式は文系の私には読むの大変だし、公開されたコードはなんだか品質が悪くて読みづらい。まぁ、彼らはプログラマーじゃなくて学者さんなのだから、コードにこだわりがないのでしょう。
というわけで、簡単に使えると評判の深層学習ライブラリのKerasと関数型プログラミングを活用して、イマドキの画像認識の計算グラフをできるだけ簡潔なコードで書いてみました。実装したのは、深さより幅というパラダイム・シフトをもたらしたWide ResNetと、少ないパラメーター数で実用的な精度が出て便利なSqueezeNetです。
実装
参考
- Deep Residual Learning for Image Recognition
Wide ResNetの元ネタのResNetの論文です。 - Identity Mappings in Deep Residual Networks
ResNetにどんな修正をすると精度が出るのか、様々な形で実験した論文です。バッチ・ノーマライゼーション→ReLU→畳み込みという定石は、ここかららしい。「試してみた」がいっぱい並んでいるので、学者さんでも結構いきあたりばったりに試していることが分かって楽しい。 - Wide Residual Network
Wide ResNetの論文です。 - SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size
SqueezeNetの論文です。 - 2016年の深層学習を用いた画像認識モデル
論文の解説と、Chainerを使用した様々な論文のニューラル・ネットワークの実装です。Chainer使いの人は、こちらのコードをコピー&ペーストで。 - 画像分類のDeep-CNNを同条件で比較してみる
Chainerを使用して、同じ条件で様々な論文のニューラル・ネットワークの精度を比較しています。Chainer使いの人は、コードが美しいので参考になると思います。
計算グラフの定義は、関数を返す関数を定義する形で
さて、計算グラフの定義と聞くと難しそうなのですけど、実際は、ただの関数の組み合わせでしかありません。add()とsubtract()という関数を使用してx + 1 - 2を表現すると、subtract(add(x, 1), 2)になるというだけ。で、深層学習はこの1や2の部分にどんな値を設定すればよいかを学習するものなので記述は不要ですから、subtract(add(x))みたいなさらに簡単な書き方になります。たとえば、バッチ・ノーマライゼーションしたあとにReLUで活性化して畳み込みをするという定石をKerasで書くと、以下のようになります。
y = Conv2D(...)(Activation('relu')(BatchNormalization()(x)))
なんかおかしな見た目をしているのは、KerasではConv2D(...)と書くと畳み込みをする計算グラフが返されて、それに引数(この場合はx)を渡す形になっているため。関数を返す関数(実際には関数として呼び出せるオブジェクトを返すコンストラクタ)ですな。一般的な言語で言うところの、ラムダ式を返す関数のような感じ。
あれ、ということは、関数合成できちゃう? a(b(c(x)))をf = compose(a, b, c); f(x)と書くアレですよ。Pythonで関数型プログラミングするときに私が使っているライブラリのfuncyにはcompose(数式みたいに右から左に合成)とrcompose(composeの逆順で合成)がありましたので、先ほどのコードを書き換えてみます。今回は、言葉での記述と順序が同じになって分かりやすいrcomposeを使用しました。
y = rcompose(BatchNormalization(),
Activation('relu'),
Conv2D(...))(x)
で、xを渡す(関数を実際に呼び出す)のはモデルを作るときまで遅らせちゃおうと考えれば、バッチ・ノーマライゼーションしてReLUして畳み込みをする計算グラフを返す関数を、以下のように定義できます。
def bn_relu_conv(filters, kernel_size, strides=1):
return rcompose(BatchNormalization(),
Activation('relu'),
Conv2D(filters, kernel_size, strides=strides, ...))
言葉での定義を、ほぼそのまま書いただけ。実にわかりやすいですな。
分岐は、juxtで
でもまぁ、この程度のことはKerasの作者さんは当然ご存知なわけで、だからKerasではSequentialという型が定義されています。Sequentialを使えば、以下のような感じで計算グラフを定義できます。
model = Sequential([BatchNormalization(),
Activation('relu'),
Conv2D(...)])
でもね、この書き方だと分岐と結合が表現できないんですよ。なので、Kerasでは関数型APIというのも提供しています。Kerasのガイドに従ってResNetのresidual unit(下図を参照。畳み込みした結果と、畳込みをしないでショートカットさせたものを足し合わせる)を定義すると、以下のようになります。
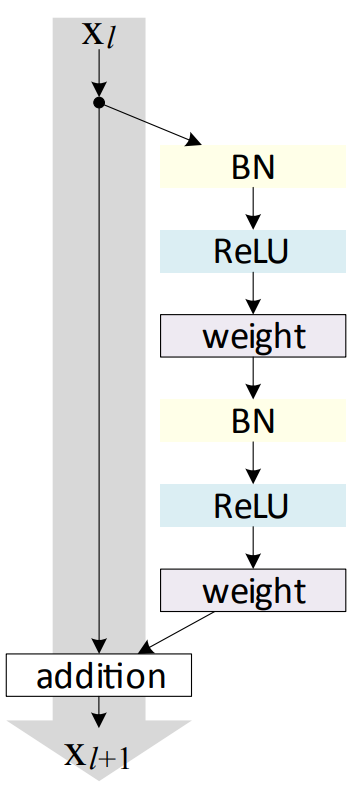
y = BatchNormalization()(x)
y = Activation('relu')(y)
y = Conv2D(64, 3, padding='same', use_bias=False)(y)
y = BatchNormalization()(y)
y = Activation('relu')(y)
y = Conv2D(64, 3, padding='same', use_bias=False)(y)
y = Add()([y, x])
ダメだ、このコードはあまりに醜い……。変数yに何度も再代入するところが特にキモチワルイ。先ほど作成したbn_relu_convを使用して関数化しても……、
def residual_unit(x, filters):
y = rcompose(bn_relu_conv(filters, 3),
bn_relu_conv(filters, 3))(x)
y = Add()([y, x])
return y
やっぱりダメ。関数の種類が2つ(xを引数に取らないで計算グラフを返す関数と、xを引数に取って計算結果を返す関数の2種類)になって、コードを読むときに脳のモードを切り替えなければならなくて、可読性が悪化していますし。
でもね、関数型プログラマーであるfuncyの作者さんは、関数合成ではこのような問題が発生することくらい、もちろんご存知でいらっしゃいます。だから素敵な解決策を用意してくれていて、それがjuxtです。
def inc(x):
return x + 1
def dec(y):
return x - 1
y = juxt(inc, dec)(10) # yは[11, 9]になります。
ただし、funcyはPython3だとジェネレーターを積極的に活用するのにKerasはジェネレーターよりもリストが好きなので、残念ですけどjuxtそのままは使えませんでした。だから、リストを返すljuxtを定義します。そうすれば、residual_unitは以下のように書けます。
def ljuxt(*fs):
return rcompose(juxt(*fs), list)
def residual_unit(filters):
return rcompose(ljuxt(rcompose(bn_relu_conv(filters, 3),
bn_relu_conv(filters, 3)),
identity),
Add())
なお、上のコードで使用しているidentityってのは引数をそのまま返す関数で、これを使えばf(x) + xをrcompose(juxt(f, identity), operator.add)で表現できるわけですね。
これで、関数の種類が1つだけになって、変数の再代入がなくなって細かい変数名を突合しなくても分岐と結合があることが明確になって、うん、可読性が上がってコードが美しい!
Wide ResNet
以上で書き方が決まりましたので、Wide ResNetを実装してみました。計算グラフを定義する部分のコードを以下に載せます。
def computational_graph(class_size):
# Utility functions.
def ljuxt(*fs):
return rcompose(juxt(*fs), list)
def batch_normalization():
return BatchNormalization()
def relu():
return Activation('relu')
def conv(filter_size, kernel_size, stride_size=1):
return Conv2D(filter_size, kernel_size, strides=stride_size, padding='same',
kernel_initializer='he_normal', kernel_regularizer=l2(0.0005), use_bias=False)
# ReLUしたいならウェイトをHe初期化するのが基本らしい。
# Kerasにはweight decayがないので、kernel_regularizerで代替しました。
def add():
return Add()
def global_average_pooling():
return GlobalAveragePooling2D()
def dense(unit_size, activation):
return Dense(unit_size, activation=activation, kernel_regularizer=l2(0.0005))
# Kerasにはweight decayがないので、kernel_regularizerで代替しました。
# Define WRN-28-10
def first_residual_unit(filter_size, stride_size):
return rcompose(batch_normalization(),
relu(),
ljuxt(rcompose(conv(filter_size, 3, stride_size),
batch_normalization(),
relu(),
conv(filter_size, 3, 1)),
rcompose(conv(filter_size, 1, stride_size))),
add())
def residual_unit(filter_size):
return rcompose(ljuxt(rcompose(batch_normalization(),
relu(),
conv(filter_size, 3),
batch_normalization(),
relu(),
conv(filter_size, 3)),
identity),
add())
def residual_block(filter_size, stride_size, unit_size):
return rcompose(first_residual_unit(filter_size, stride_size),
rcompose(*repeatedly(partial(residual_unit, filter_size), unit_size - 1)))
k = 10 # 論文によれば、CIFAR-10に最適な値は10。
n = 4 # 論文によれば、CIFAR-10に最適な値は4。
# WRN-28なのに4になっているのは、28はdepthで、depthはconvの数で、1(最初のconv)+ 3 * n * 2 + 3(ショートカットのconv?)だからみたい。
return rcompose(conv(16, 3),
residual_block(16 * k, 1, n),
residual_block(32 * k, 2, n),
residual_block(64 * k, 2, n),
batch_normalization(),
relu(),
global_average_pooling(),
dense(class_size, 'softmax'))
うん、簡単ですな。どんな計算グラフなのかが、コードからすぐに読み取れます。なお、上のコードでバッチ・ノーマライゼーション→ReLU→畳み込みを関数にまとめていないのは、Deep Pyramidal Redisual Networksの3.3.1に書いてあるように、residual blockの最初のReLUを削って最後にバッチ・ノーマライゼーションを追加するとさらに精度が向上するらしいから。今後もこういう細かい変化が出てくると思うんですよね。
ちなみに、Wide ResNetはこんな感じの計算グラフです(Wide ResNetの元ネタのResNet論文の画像なので、少し異なりますけど)。

SqueezeNet
SqueezeNetは、こんな感じ。
def computational_graph(class_size):
# Utility functions.
def ljuxt(*fs):
return rcompose(juxt(*fs), list)
def batch_normalization():
return BatchNormalization()
def relu():
return Activation('relu')
def conv(filters, kernel_size):
return Conv2D(filters, kernel_size, padding='same', kernel_initializer='he_normal', kernel_regularizer=l2(0.0001))
def concatenate():
return Concatenate()
def add():
return Add()
def max_pooling():
return MaxPooling2D()
def dropout():
return Dropout(0.5)
def global_average_pooling():
return GlobalAveragePooling2D()
def softmax():
return Activation('softmax')
# Define SqueezeNet.
def fire_module(filters_squeeze, filters_expand):
return rcompose(batch_normalization(),
relu(),
conv(filters_squeeze, 1),
batch_normalization(),
relu(),
ljuxt(conv(filters_expand // 2, 1),
conv(filters_expand // 2, 3)),
concatenate())
def fire_module_with_shortcut(filters_squeeze, filters_expand):
return rcompose(ljuxt(fire_module(filters_squeeze, filters_expand),
identity),
add())
return rcompose(conv(96, 3),
max_pooling(),
fire_module(16, 128),
fire_module_with_shortcut(16, 128),
fire_module(32, 256),
max_pooling(),
fire_module_with_shortcut(32, 256),
fire_module(48, 384),
fire_module_with_shortcut(48, 384),
fire_module(64, 512),
max_pooling(),
fire_module_with_shortcut(64, 512),
batch_normalization(),
relu(),
conv(class_size, 1),
global_average_pooling(),
softmax())
ちなみに、SqueezeNetはこんな感じの計算グラフです。
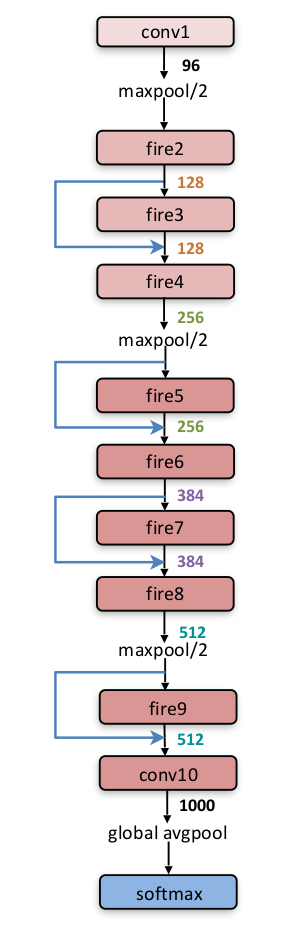
fireと書かれている部分の構造は以下のような感じ。
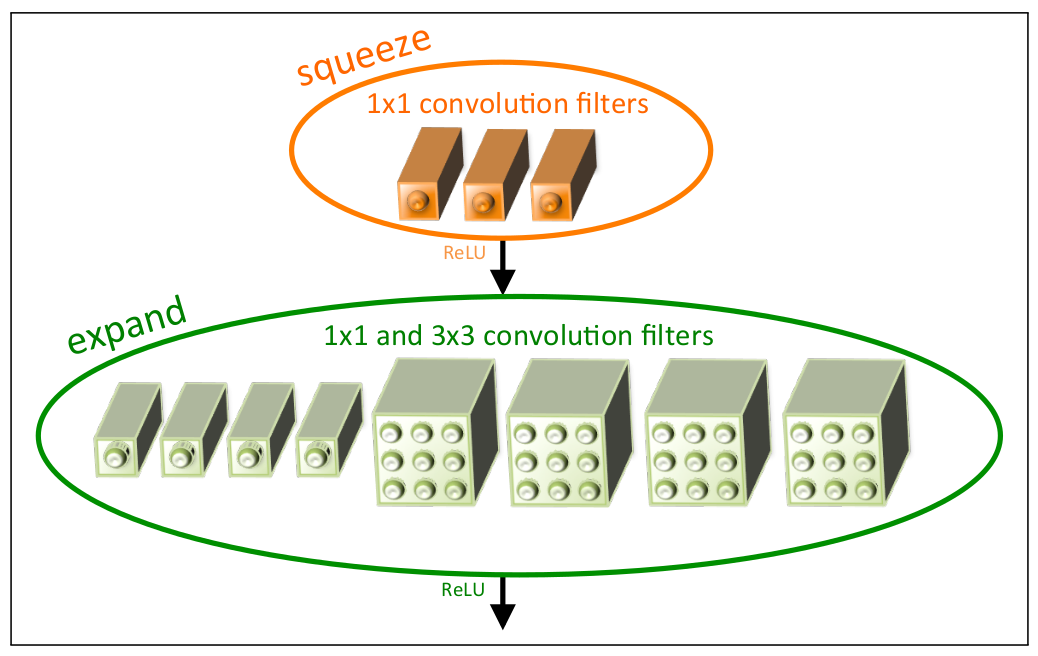
えっと、論文だとSqueezeNetは浮動小数点のビット数を減らしても精度が下がらないと書かれていてスゴそうだったのですけど、浮動小数点の精度を下げる方法が分からなかったので試していません。中途半端でごめんなさい……。
なにはともあれ
関数型プログラミング最高! Kerasとfuncyとnutszebraさんとtakedartsさんありがとー!