2018/06/20
今年49歳になるおっさんでも作れたAlphaZero
前回やったモンテカルロ木探索は、けっこう強くて面白かった。でも、人間の欲には限りがありません。もう少しだけ、強くできないかな? それ、話題の深層学習ならできます。そう、AlphaGoの後継のAlphaZeroならね。
#作成したコードはこちら。
モンテカルロ木探索で、なんとなく不満なところ
モンテカルロ木探索では、UCB1というアルゴリズムで手を選んでいました。で、このUCB1なんですけど、とりあえず1回は全部の手を試すところが嫌じゃないですか? 相手がリーチをかけてきたら、防ぐ以外の手は考えられません。でもUCB1だとそれ以外の手も試さなければならないという……。会社で明らかにダメなプロダクトを使えと言われて、いかにダメかを口頭で説明して、でも意識高げな詐欺師に騙されちゃってるみたいで聞く耳持ってもらえなくて無駄な評価作業を開始するときのような感じ。プログラム組めない奴がプロダクトを選定するの禁止しろよ! 関数型言語による生産性向上率を測定しろというような、技術的に正しい作業をしたいなぁ……。
で、プロダクト選定はともかくとして、局面を入力にしてどの手を選ぶべきかを出力する程度なら、深層学習でできるんですよ。だって、写真に写っているのが飛行機か自動車か鳥か猫か鹿か犬か蛙か馬か船かトラックなのかを出力できちゃうのですから、局面を入力に次に指すべきマスが左上か中央上か右上か残りのどこかなのかを出力するぐらいできて当たり前。精度はそれほど高くなくて、間違えまくるでしょうけど。
あと、プレイアウトを繰り返して局面の価値を測定するのも、なんだか処理が重そうで嫌じゃないですか? ダブル・リーチをかけられたら、考えるまでもなく最悪の局面なはず。でも、何度もプレイアウトしてどれだけ悪いかを確かめなければなりません。同じシステムを何度も作るみたいな感じ。経験がないプログラミング言語を使ってよいなら、同じシステムでも勉強になるので大歓迎ですけど。みんな一度はClojureをやってみると良いと思うよ。あれは、いいものだ。
でね、システムを作るのは無理ですけど、局面を入力にして価値を出力する程度なら、深層学習でできるんですよ。だって、写真を入力にインスタグラムでいいねがもらえるかどうかを出力できちゃうんですから。局面を入力に+1.0から-1.0の間の数値を出力するなんて朝飯前です。精度が足りなくて、良いと出力された局面を選んだのに窮地に追い込まれたりするでしょうけど。
まとめます。深層学習なら、次にどの手を指すべきかとか、局面の価値とかを出力することだできます。でも、今のところ、精度はあまり高くありません。AlphaGoの開発で、あのGoogle様が頑張っても、次の一手が人間の強いプレイヤーと一致する確率は57%程度だったそうです。だから、深層学習の出力をただ使うだけでは、そんなに強くはなりません。でも、この2つの値をモンテカルロ木探索に組み込んだら?
モンテカルロ木探索への組み込み
とりあえず、深層学習で次の一手と局面の価値を出力できるものとしてください。predict()という関数があって、その関数は深層学習の魔法でアクション毎の推奨度(Googleはポリシーと読んでいるので、以後ポリシー)と、局面の価値を返すものとします。
>>> predict(State())
([0.1, 0.6, 0.1, 0.05, 0.02, 0.03, 0.1, 0.0, 0.0], 0.78) # [0.1...]がポリシー。アクション単位での確率です。0.78が局面の価値。仮なので、でたらめな値ですけど
このpredict()関数を使う、モンテカルロ木探索のコードを考えてみます。最初に問題になるのはポリシーを考慮していないUCB1の部分ですけど、幸いなことに、Googleが式を定義してくれました。
w / n + C_PUCT * p * sqrt(t) / (1 + n)
# wはこのノードの価値
# nはこのノードの評価回数
# C_PUCTはバランスを調整するための定数。とりあえず1.0でよいみたい。
# pはポリシー
# tは総評価回数
……どうしてUCB1と大きく違うんだろ? 数学上の秘密があるのでしょうけど、どうせ49歳のおっさんな私には理解できませんから、この式をそのまま使います。UCB1のlogより、この式のsqrtの方が少しだけ馴染みがありますしね。プログラム面では、ポリシーのpをnodeクラスに追加する程度の影響しかないですし。
残る作業は、playout()の代わりにpredict()を呼び出すように変更して、ルート・ノードもポリシーを取得するためにpredict()を呼び出すからexpand()をメソッドとして切り出すのをやめるだけ。さっそく作ってみましょう。
class node:
def __init__(self, state, p):
self.state = state
self.p = p # 方策
self.w = 0 # 価値
self.n = 0 # 試行回数
self.child_nodes = None # 子ノード
def evaluate(self):
if self.state.end:
value = -1 if self.state.lose else 0
self.w += value
self.n += 1
return value
if not self.child_nodes:
policies, value = predict(model, self.state)
self.w += value
self.n += 1
self.child_nodes = tuple(node(self.state.next(action), policy) for action, policy in zip(self.state.legal_actions, policies))
return value
else:
value = -self.next_child_node().evaluate()
self.w += value
self.n += 1
return value
def next_child_node(self):
def pucb_values():
t = sum(map(attrgetter('n'), self.child_nodes))
# child_node.nが0の場合に大きな値を設定してしまうと結局全部の手を試してみることになってしまうので、-1から1の中央の0を設定しました。
return tuple((-child_node.w / child_node.n if child_node.n else 0.0) + C_PUCT * child_node.p * sqrt(t) / (1 + child_node.n) for child_node in self.child_nodes)
return self.child_nodes[np.argmax(pucb_values())]
お時間があったら、前回のモンテカルロ木探索のコードと見比べてみてください。モンテカルロ木探索のコードとほとんど同じで、むしろ単純になっています。predict()の第一引数のmodelは深層学習のモデルで、深層学習で処理するときに必要になるモノです。とりあえず無視してください。
ただ、このnodeクラスを「使う」部分は、少し複雑です。というのも、深層学習には「学習」って名前がついていて、コンピューターにおける学習ってのは大量のデータを食わせていく作業を指すので、そのデータを作るための工夫が必要なんですよ。
強化学習
もし、あなたがマルバツの棋譜を数万枚持っているなら、その棋譜をデータ化して学習させることが可能です。その場合は、モンテカルロ木探索の場合と同様にnodeクラスのnを使って次の一手を返す関数を作ればオッケー。でも、私はそんなマニアックな棋譜は持っていませんから、コンピューターに学習データを生成させることにしました。
学習に必要なデータは入力と出力のペアで、今回は、入力が局面で出力がポリシーと価値です。学習とは、こんな入力のときはこんな出力が正解だからねってのを繰り返しコンピューターに教え込んでいく作業なんですよ。で、入力の局面はよいとして、出力であるポリシーと価値の正解データはどうしましょうか? ポリシーも価値も正解が分からないから、それを探索するプログラムを組んでいるのに……。
で、単純すぎてビックリなのですけど、勝った場合はその勝ちに至る局面の「価値」を1、負けた場合は-1を正解としちゃっていいんだそうです。学習後にさらに対戦させてデータをとって、そのデータでさらに学習させてさらにさらに対戦させてデータを取って……ってのを繰り返してよいなら、こんなに単純なやり方でも多くの場合でうまくいくみたい。でも、「ポリシー」はどうしましょうか? 勝った手のポリシーを増やして、負けた手のポリシーは減らすのかな? 増やしたり減したりといっても、どれくらいがよいの?
にわかには信じられないのですけど、今回の対戦で得たモンテカルロ木探索のnの値を正解にしちゃえばよいらしい。考えてみましょう。勝ったにせよ負けたにせよnの値はモンテカルロ木探索を頑張った結果なわけで、深く読むべき局面と浅く読むべき局面を表現している、正解に近い値だと考えることができます。あと、価値が正しく設定されるなら、その価値に沿う形に次回の対戦でのnが変わって、次は今よりもさらに正解に近い値となるはずです。
ともあれ、学習するにはnの値を保存しておかなければならないことが分かったわけで、だからまずはnの値を返す関数を作ります。
def pv_mcts_scores(model, evaluate_count, state):
# 先程のnodeクラスは、ここに入ります。これでpredict()の引数のmodelは、引数のmodelがそのまま使われます。
root_node = node(state, 0)
for _ in range(evaluate_count):
root_node.evaluate()
return tuple(map(attrgetter('n'), root_node.child_nodes))
関数名の先頭のPVはPolicy Valueの意味で、MCTSはMonte Carlo Tree Searchの意味です(AlphaZeroのアルゴリズムは、この前に更にAsynchronous(非同期)のAがついたAPV MCTSと呼ぶみたい)。見ての通り、この関数はnそのものを返します。
で、もう一つ。学習をさせるには、ランダム性の追加をしなければなりません。深層学習では、入力が同じであれば同じ結果を出力します。マルバツの最初の局面は毎回同じ(何も記入されていない空の盤面)なので、それを入力にしたpredict()の出力も毎回同じになります。そして今回作成したコード中にはランダムは含まれませんから、pv_mcts_scores()の戻り値も、やはり毎回同じになります……。これでは何回対戦しても同じ棋譜しか得られなくて、学習が成り立ちません。どうにかしてランダム性を追加して、学習データのバリエーションを増やしたい。
すぐに思いつくのは時々ランダムで適当な手を選ぶ方式(εグリーディという大層な名前がついています)ですけど、AlphaZeroはそれより良い方式を採用しています。nの値を確率とみなして、確率的に手を選ぶという方式です。でも、本番の試合では、最高の手だけを指して欲しいですよね? あと、学習データを作成する場合でも、学習初期はランダム性を大きく設定したバリエーションが豊富なデータが、学習の後期にはランダム性を小さくした精度の高いデータが欲しかったりするかもしれません。
こんなワガママを叶えるためにAlphaZeroが採用したのが、ボルツマン分布ってやつみたい。で、ボルツマン分布の式を見たのですけど私では全く理解できなかったので、GitHubを検索して見つけた中で一番分かりやすかったコードを入れてみました。
def boltzman(xs, temperature):
xs = [x ** (1 / temperature) for x in xs]
return [x / sum(xs) for x in xs]
このコードなら、温度が1ならば確率通りで、温度が下がっていくといい感じに格差が広がっていきそうです。温度がゼロの場合には例外が出ますけど、温度を0にしたいのは本番の試合だけで、本番ではなにもこんな面倒な関数を通さずに単純にargmaxしちゃえばオッケー。なので、temperatureが0の場合は無視して、本番でnext_actionするための関数を書きます。
def pv_mcts_next_action_fn(model):
def pv_mcts_next_action(state):
return state.legal_actions[np.argmax(pv_mcts_scores(model, 20, state))]
return pv_mcts_next_action
試合の際に必要なのはstateだけを引数にする関数で、でも、pv_mcts_scores()にはそれ以外の引数が必要だったので、関数を返す関数として作成しました。関数型プログラミングって本当に便利ですな。そうそう、プレイアウトが不要になる分だけ深く読めるはずなので、試行回数はテキトーに減らしておきました。
深層学習
では、このあたりで先送りにしてきた深層学習絡みの部分を。
深層学習ってのは脳のニューロンを模した構造を、処理が楽になるようにベクトル演算で実現して、で、ベクトルつながりで画像処理のフィルター(深層学習では、何故か畳み込みと呼びます)を組み入れた結果、脳ともニューロンともあまり関係がなくなったように見えるニューラル・ネットワークで処理します。このニューラル・ネットワークを使う場合のプログラムへの最も大きな影響は、入力も出力も固定長の数値のベクトルになるということ。数値で表現できないものはダメですし、たとえ数値であってもゲームの合法手のような局面によって数が変わる可変長な情報そのままも扱えません。
マルバツはここまで数値で表現できているので数値問題はクリアなのですけど、固定長問題は解決が必要です。なので、贅沢ですけど最大の場合の長さを使うことにしましょう。マルバツの場合で言うと、ポリシーを長さ9のベクトルにしちゃうわけ。価値は長さ1のベクトル。幸いなことに、マルバツの局面は3✕3✕2の固定長にできます(「3✕3」は盤面の縦と横で、「✕2」は自分と敵)にできます。マルやバツが書き込まれたマスは1、そうでないマスは0となります)。「マルは「1」でバツは「2」にすれば3✕3だけで済んで経済的じゃん」って考え方は、深層学習ではダメ。というのも、先程単語が出てきた畳み込みってのが、何らかの量を表現しているものが順序よく並んでいる場合にだけ使えるテクニックなんですよ。バツはマルの2倍などという関係はありませんので、分割して同じに扱わなければなりません。畳み込みの元になった画像処理の画像データでも、青と赤と緑を別の数値で表現するでしょ?
というわけで、今回作成するニューラル・ネットワークの入力と出力は、以下の図のようになりました。
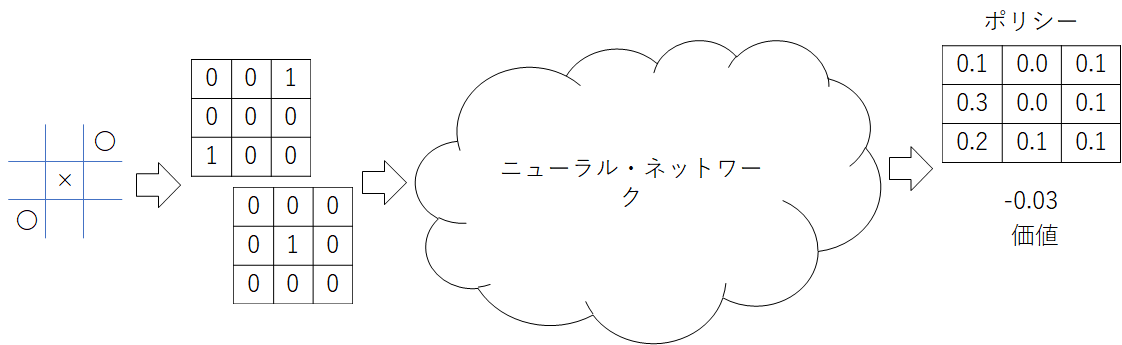
あとはニューラル・ネットワークの中身を決めるだけ……なんですけど、AlphaZeroのニューラル・ネットワークが採用したResidual Networkってのは数年前から大流行しているごく当たり前の構造なので、特別に説明するような事柄がないんですよね。過去にKerasでのコードを作っていましたので、そこから適当にコピー&ペーストしました。
from funcy import *
from keras.layers import Activation, Add, BatchNormalization, Conv2D, Dense, GlobalAveragePooling2D, Input
from keras.models import Model, save_model
from keras.regularizers import l2
def computational_graph():
WIDTH = 128 # AlphaZeroでは256。
HEIGHT = 16 # AlphaZeroでは19。
def ljuxt(*fs):
return rcompose(juxt(*fs), list)
def add():
return Add()
def batch_normalization():
return BatchNormalization()
def conv(channel_size):
return Conv2D(channel_size, 3, padding='same', use_bias=False, kernel_initializer='he_normal', kernel_regularizer=l2(0.0005))
def dense(unit_size):
return Dense(unit_size, kernel_regularizer=l2(0.0005))
def global_average_pooling():
return GlobalAveragePooling2D()
def relu():
return Activation('relu')
def softmax():
return Activation('softmax')
def tanh():
return Activation('tanh')
def residual_block():
return rcompose(ljuxt(rcompose(batch_normalization(),
conv(WIDTH),
batch_normalization(),
relu(),
conv(WIDTH),
batch_normalization()),
identity),
add())
return rcompose(conv(WIDTH),
rcompose(*repeatedly(residual_block, HEIGHT)),
global_average_pooling(),
ljuxt(rcompose(dense(9)),
rcompose(dense(1), tanh())))
ニューラル・ネットワークという名前を使うのはちょっと恥ずかしいので、関数名はcomputational_graph()、計算グラフにしました。こんな簡単なコードですけど、これでResidual Networkは完成です。出力が固定長云々に対応しているのは最後の2行で、dense(9)でポリシー用の長さ9のベクトルを、dense(1)で価値用の長さ1のベクトルを作成しています(AlphaZeroではこの部分も多段になっているみたいですけど、マルバツは簡単なので1層にしちゃいました)。ポリシーについては、dense()の結果をそのまま出力にします。一般的にはこのあとに何らかの活性化関数を入れるのですけど、合法手以外のポリシーは使わないわけで、非合法な手を含んでいる今はできることがありませんから。価値は-1から1の値になっていて欲しいので、tanhを使用しました。あと、なんかやけにコードがスッキリしているなぁって感じるのは、関数型プログラミングのテクニックを使っているからです。詳細はここで。
で、この計算グラフから処理を呼び出す際に必要となるモデルを作成するコードは、以下の通り。
model = Model(*juxt(identity, computational_graph())(Input(shape=(3, 3, 2))))
入力の3✕3✕2に相当するのが、shape=(3, 3, 2)の部分です。
今回は、モデルを作る、そのモデルを使うPV MCTSで対戦して学習データを溜める、溜めた学習データを使ってモデルを学習させる……というステップを踏みますから、深層学習のサンプル・コードみたいにモデルを作成したら即学習ってわけにはいきません。だから、とりあえず、このモデルは保存して終わりにしちゃいましょう。
save_model(model, './model/0000.h5')
……えっと、保存するのは1個だけでよいのかな? 皆様、これまでの説明を読んでいるときに「本当にそんな簡単な仕組みでうまく行くの?」という疑念がわきませんでしたか? 実はその疑念は正しくて、やってみるとうまく行ったりうまく行かなかったりするんです。データを溜めて学習させたらかえって弱くなっちゃった、みたいな感じ。この事態への対策として、訓練用の候補生を別途保存しておくことにしましょう。
save_model(model, './model/candidate/0000.h5')
チャンピオン同士を対戦させてデータを作成して、そのデータで候補生を訓練して、そしてチャンピオンと候補生を戦わせて勝った方を次のチャンピオンにする仕組みです。学習一回の単位で見ると強くなったり弱くなったりするんですけど、傾向としてはだんだん強くなっていくので、このやり方なら最強のチャンピオンが残り続けるはず。
あとは、後回しにしていたpredict()を実装しておきましょう。
import numpy as np
from funcy import *
def to_x(state):
def pieces_to_x(pieces):
return (1.0 if pieces & 0b100000000 >> i else 0.0 for i in range(9))
return np.array(tuple(mapcat(pieces_to_x, (state.pieces, state.enemy_pieces)))).reshape(2, 3, 3).transpose(1, 2, 0)
def predict(model, state):
x = to_x(state).reshape(1, 3, 3, 2)
y = model.predict(x, batch_size=1)
policies = y[0][0][list(state.legal_actions)]
policies /= sum(policies) if sum(policies) else 1
return policies, y[1][0][0]
to_x()は入力用の3✕3✕2の行列を作る関数です(Kerasでは、入力をx、出力をyと名付ける慣習があるみたい)。上のコードで使用しているNumPyは、癖があって時々辛いけど、とてもとても便利です。たとえばNumPyのarrayではarray[(1, 3, 4)]と書くと[array[1], array[3], array[4]]が返ってくる機能があって、それを利用しているのがpoliciesに値を代入する部分のy[0][0][list(state.legal_actions)]です。これだけで、ニューラル・ネットワークの制限に縛られた固定長のベクトルから、可変長な合法手それぞれのポリシーに変換されます。で、今回は手の確率にしておきたい(そうしないと、next_child_node()の式た正しく動かない気がする)ので、合計値で割り算しています。あと、ニューラル・ネットワークの出力はベクトル2つのはずなのに添字が一個多く見えるのは、ニューラル・ネットワークでは複数の処理をバッチとして処理するため。今回はbatch_size=1なので、2つ目の添字に無条件で[0]を指定しました。入力のxの方も、reshape()で先頭に1を追加しています。
セルフ・プレイ
では、データ取りのためにチャンピオン同士に対戦してもらいましょう。学習データの保存には、Pythonのpickleを使用しました。入力(の元)となるstatesと、出力の正解となるysを生成して、pickleで保存します。
import numpy as np
import pickle
from datetime import datetime
from funcy import *
from keras.models import load_model
from pathlib import Path
from pv_mcts import boltzman, pv_mcts_scores
from tictactoe import State, popcount
MAX_GAME_COUNT = 500 # AlphaZeroでは25000。
MCTS_EVALUATE_COUNT = 20 # AlphaZeroでは1600。
TEMPERATURE = 1.0
def first_player_value(ended_state):
if ended_state.lose:
return 1 if (popcount(ended_state.pieces) + popcount(ended_state.enemy_pieces)) % 2 == 1 else -1
return 0
def play(model):
states = []
ys = [[], None]
state = State()
while True:
if state.end:
break
scores = pv_mcts_scores(model, MCTS_EVALUATE_COUNT, state)
policies = [0] * 9
for action, policy in zip(state.legal_actions, boltzman(scores, 1.0)):
policies[action] = policy
states.append(state)
ys[0].append(policies)
state = state.next(np.random.choice(state.legal_actions, p=boltzman(scores, TEMPERATURE)))
value = first_player_value(state)
ys[1] = tuple(take(len(ys[0]), cycle((value, -value))))
return states, ys
def write_data(states, ys, game_count):
y_policies, y_values = ys
now = datetime.now()
for i in range(len(states)):
with open('./data/{:04}-{:02}-{:02}-{:02}-{:02}-{:02}-{:04}-{:02}.pickle'.format(now.year, now.month, now.day, now.hour, now.minute, now.second, game_count, i), mode='wb') as f:
pickle.dump((states[i], y_policies[i], y_values[i]), f)
def main():
model = load_model(last(sorted(Path('./model').glob('*.h5'))))
for i in range(MAX_GAME_COUNT):
states, ys = play(model)
print('*** game {:03}/{:03} ended at {} ***'.format(i + 1, MAX_GAME_COUNT, datetime.now()))
print(states[-1])
write_data(states, ys, i)
if __name__ == '__main__':
main()
うーん、特に書くことないなぁ……。あ、ごめんなさい。面倒だったので、ボルツマン分布の温度は1.0固定にしてしまいました。
学習
先程のプログラムを実行すると学習データができますから、そのデータを使って学習させましょう。といっても作業の殆どはKerasがやってくれますから、とても簡単です。
import numpy as np
import pickle
from funcy import *
from keras.callbacks import LearningRateScheduler
from keras.models import load_model, save_model
from pathlib import Path
from pv_mcts import to_x
from operator import getitem
def load_data():
def load_datum(path):
with path.open(mode='rb') as f:
return pickle.load(f)
states, y_policies, y_values = zip(*map(load_datum, tuple(sorted(Path('./data').glob('*.pickle')))[-5000:])) # AlphaZeroはランダムで抽出。
return map(np.array, (tuple(map(to_x, states)), y_policies, y_values))
def main():
xs, y_policies, y_values = load_data()
model_path = last(sorted(Path('./model/candidate').glob('*.h5')))
model = load_model(model_path)
model.compile(loss=['mean_squared_error', 'mean_squared_error'], optimizer='adam')
model.fit(xs, [y_policies, y_values], 100, 100,
callbacks=[LearningRateScheduler(partial(getitem, tuple(take(100, concat(repeat(0.001, 50), repeat(0.0005, 25), repeat(0.00025))))))])
save_model(model, model_path.with_name('{:04}.h5'.format(int(model_path.stem) + 1)))
if __name__ == '__main__':
main()
はい、これだけ。AlphaZeroはSGDというオプティマイザーを使ったらしいのですけど、私はTensorFlowのチュートリアルが使っていたAdamを使用しました。だって、Adamだと学習が速いんだもん。数式が分からなかったので速い理由はカケラも分かってないけどな。損失関数は、フィーリングで二乗誤差にしています。あと、学習率を少しずつ下げるコールバックをテキトーに設定しました。最高の精度を実現して論文書いてやるぜって場合じゃなければ、テキトーでもそれなりの精度が出るんですよ。
評価
あとは、学習させた候補とチャンピオンの対戦です。といっても、セルフ・プレイからデータ保存の部分を抜いて、勝率を調べる処理を追加した程度です。
import numpy as np
from datetime import datetime
from funcy import *
from keras.models import load_model
from pathlib import Path
from pv_mcts import boltzman, pv_mcts_scores
from shutil import copy
from tictactoe import State, popcount
MAX_GAME_COUNT = 100 # AlphaZeroでは400。
MCTS_EVALUATE_COUNT = 20 # AlphaZeroでは1600。
TEMPERATURE = 1.0
def first_player_point(ended_state):
if ended_state.lose:
return 1 if (popcount(ended_state.pieces) + popcount(ended_state.enemy_pieces)) % 2 == 1 else 0
return 0.5
def play(models):
state = State()
for model in cycle(models):
if state.end:
break;
state = state.next(np.random.choice(state.legal_actions, p=boltzman(pv_mcts_scores(model, MCTS_EVALUATE_COUNT, state), TEMPERATURE)))
return first_player_point(state)
def update_model():
challenger_path = last(sorted(Path('./model/candidate').glob('*.h5')))
champion_path = last(sorted(Path('./model').glob('*.h5')))
copy(str(challenger_path), str(champion_path.with_name(challenger_path.name)))
def main():
models = tuple(map(lambda path: load_model(last(sorted(path.glob('*.h5')))), (Path('./model/candidate'), Path('./model'))))
total_point = 0
for i in range(MAX_GAME_COUNT):
if i % 2 == 0:
total_point += play(models)
else:
total_point += 1 - play(tuple(reversed(models)))
print('*** game {:03}/{:03} ended at {} ***'.format(i + 1, MAX_GAME_COUNT, datetime.now()))
print(total_point / (i + 1))
average_point = total_point / MAX_GAME_COUNT
print(average_point)
if average_point > 0.5: # AlphaZeroでは0.55。マルバツだと最善同士で引き分けになるので、ちょっと下げてみました。
update_model()
if __name__ == '__main__':
main()
……コードの重複を排除していなくてごめんなさい。セルフ・プレイとほとんど同じなので、どーにも書くことがありません。あ、AlphaZeroでは勝率が55%を超えたら入れ替えだったのですけど、マルバツだと最強AI同士の対戦で勝率50パーセントになるので、50パーセントを超えたら入れ替えに変更しました。
実行
これでプログラムはすべて完成です。実行してみましょう。モデル作成のコードをinitialize.py、セルフ・プレイをself_play.py、学習をtrain.py、評価をevaluate.pyという名前で保存して、以下のシェル・プログラムで実行させます。
#!/bin/sh
python initialize.py
for i in `seq 1 10` ; do
python self_play.py
python train.py
python evaluate.py
done
とりあえず、10サイクル回してみましょう。NVIDIA GTX 1080 TiをThunderbolt 3で繋いだ私のラップトップPCで、2時間くらいかかりました。
で、成果は?
サイクルが回ったので、どれくらい強くなったのか試してみる……前に、少し待って。
PV MCTSにはランダム性がなくて、だから、同様にランダム性がないアルファ・ベータ法と前回のように何回も対戦させても無意味です。あと、さっき知ったのですけど、ミスをする可能性があるプレイヤーの場合、マルバツは先手が有利なんですね。先手は初手でどこを指しても最悪でも引き分けに持ち込めるのですけど、後手は先手に合わせた適切な手を指さないと負けが決まってしまう(Wikipediaでさっき勉強しました)。そもそも、先手は先に動けますし、最後に余分に一手指せますし。
というわけで、検証方法を変更しましょう。まずは、どこまで正確に指せるのかを調べることにします。
from funcy import *
from keras.models import load_model
from pathlib import Path
from pv_mcts import pv_mcts_next_action_fn
from tictactoe import State, popcount, random_next_action, monte_carlo_tree_search_next_action, nega_alpha_next_action
def main():
def test_correctness(next_action):
return ((next_action(State().next(0)) in (4,)) +
(next_action(State().next(2)) in (4,)) +
(next_action(State().next(6)) in (4,)) +
(next_action(State().next(8)) in (4,)) +
(next_action(State().next(4)) in (0, 2, 6, 8)) +
(next_action(State().next(1)) in (0, 2, 4, 7)) +
(next_action(State().next(3)) in (0, 4, 5, 6)) +
(next_action(State().next(5)) in (2, 3, 4, 8)) +
(next_action(State().next(7)) in (1, 4, 6, 8)) +
(next_action(State().next(0).next(4).next(8)) in (1, 3, 5, 7)) +
(next_action(State().next(2).next(4).next(6)) in (1, 3, 5, 7)))
pv_mcts_next_action = pv_mcts_next_action_fn(load_model(last(sorted(Path('./model').glob('*.h5')))))
nega_alpha_correctness = test_correctness(nega_alpha_next_action)
print('{:4.1f}/11 = {:.2f} nega_alpha'.format(nega_alpha_correctness, nega_alpha_correctness / 11))
pv_mcts_correctness = test_correctness(pv_mcts_next_action)
print('{:4.1f}/11 = {:.2f} pv_mcts'.format(pv_mcts_correctness, pv_mcts_correctness / 11))
monte_carlo_tree_search_correctness = sum(map(lambda _: test_correctness(monte_carlo_tree_search_next_action), range(100))) / 100
print('{:4.1f}/11 = {:.2f} monte_carlo_tree_search'.format(monte_carlo_tree_search_correctness, monte_carlo_tree_search_correctness / 11))
で、試してみると……。
$ python test_corrctness.py
11.0/11 = 1.00 nega_alpha
10.0/11 = 0.91 pv_mcts
5.9/11 = 0.54 monte_carlo_tree_search
惜しい……。1つだけ間違えちゃいました(深層学習のニューラル・ネットワークの初期値はランダムなので、初期値ガチャを頑張ればパーフェクトになりますけど)。まぁ、モンテカルロ木探索よりも遥かに優秀なので良し! ついでですから、先手と後手を入れ替えながらのモンテカルロ木探索との対戦もやってみましょう。
print(test_algorithm((pv_mcts_next_action, monte_carlo_tree_search_next_action)))
print(test_algorithm((monte_carlo_tree_search_next_action, pv_mcts_next_action)))
0.91 # PV MCTSが先手の場合の、先手の勝率
0.575 # モンテカルロ木探索が先手の場合の、先手の勝率
うん、かなり手を抜いた簡易実装なのに、モンテカルロ木探索よりも強いです。念の為、更にサイクルを回してみましょう。一日かけて、あと90回、合計して100回のサイクルを回してみました。
11.0/11 = 1.00 nega_alpha
11.0/11 = 1.00 pv_mcts
6.2/11 = 0.56 monte_carlo_tree_search
0.94 # PV MCTSが先手の場合の、先手の勝率
0.515 # モンテカルロ木探索が先手の場合の、先手の勝率
やりました! パーフェクトです! 対モンテカルロ木探索の勝率も上がりました! 今年49歳になるおっさんでも作れちゃうくらいに簡単なのに、AlphaZeroってすげー。
2018/06/19
今年49歳になるおっさんが頑張って作ったモンテカルロ木探索
前回はミニ・マックス法とアルファ・ベータ法をやったのですけど、マルバツのような簡単なゲームならともかく、一般のゲームでは最後まで読みきるのは不可能なので、評価関数を作らなければなりません。でも、今年49歳になるおっさんの私は脳が弱っているので、ゲームに勝てるスゴイ評価関数を作るのは無理……。というわけで、評価関数が不要と評判のモンテカルロ木探索をやってみました。
モンテカルロ法
モンテカルロ法と聞くと大層な話に聞こえるかもしれませんけど、要はただのランダムです。ランダムな値を使用して何度もシミュレーションして、それで解を導くというだけの話。たとえば円周率の値を知りたいなら数学が得意な友人に聞くのが正攻法なのでしょうけど、私のような人間の友人がいない引きこもりには不可能です。だから、無機物の友人であるコンピューターにランダムで点を打たせて、その点が円の内側か外側かを調べて、そこから円周率を計算します。このチカラワザなやり方が、モンテカルロ法なんです。
from random import random
def main():
c = 10000000
n = 0
for _ in range(c):
# ランダムな点を作ります。
x = random() * 2 - 1
y = random() * 2 - 1
# 円の内側かどうかを判定します。
if x ** 2 + y ** 2 < 1:
n += 1
print(4 * n / c)
このプログラムを実行したところ、3.1410432が出力されました。人間の友人がいる人は、この値が正しいか確認してみてください。たぶん、小数点以下第三位くらいまでは正しいんじゃないかな。
原始モンテカルロ探索
というわけでこの名前がかっこいいモンテカルロ法の、実際はただランダムを使ってシミュレーションするだけのマルバツAIを作成してみましょう。ランダムな手でゲームを最後までシミュレーションするのを繰り返して、最も勝ちが多かった手を選ぶことにします。
# プレイアウト。
def playout(state):
if state.lose:
return -1
if state.draw:
return 0
return -playout(state.next(random_next_action(state)))
# 集合の最大値のインデックスを返します。
def argmax(collection, key=None):
return collection.index(max(collection, key=key) if key else max(collection))
# 原始モンテカルロ探索。
def monte_carlo_search_next_action(state):
values = [0] * len(state.legal_actions)
for i, action in enumerate(state.legal_actions):
for _ in range(10):
values[i] += -playout(state.next(action))
return state.legal_actions[argmax(values)]
ゲームを最後までやりきることを、業界用語ではプレイアウトというそうです。なので、playoutという名前の関数を作りました。前回作成したrandom_next_actionを使用して、勝負がつくまでゲームをやりきります。
argmaxは、集合の中の最大値のインデックスを返す関数です。たとえばargmax((2, 5, 3))なら「1」が返ってきます。この関数は、最も勝率が高かったのは何番目のアクションなのかを調べるために使用します。
で、monte_carlo_search_next_actionが、モンテカルロ法を活用した原始モンテカルロ探索と呼ばれるアルゴリズムです。今回はアクションごとに10回プレイアウトして(-playout()になっているのは、state.next()を引数にしているので、敵のスコアが返ってくるから)、プレイアウトで得たスコアの合計が最も大きなアクションを選んでいるだけ。
で、面白いことに、こんなヘッポコなコードでも、それなりの性能が出ちゃうんですよ。メイン・ルーチンを以下に変えて試してみます。
def main():
def first_player_point(ended_state):
if ended_state.lose:
return 1 if (popcount(ended_state.pieces) + popcount(ended_state.enemy_pieces)) % 2 == 1 else 0
return 0.5
def test_algorithm(next_actions):
total_point = 0
for _ in range(100):
state = State()
for next_action in cat(repeat(next_actions)):
if state.end:
break;
state = state.next(next_action(state))
total_point += first_player_point(state)
return total_point / 100
print(test_algorithm((monte_carlo_search_next_action, random_next_action)))
print(test_algorithm((monte_carlo_search_next_action, nega_alpha_next_action)))
原始モンカルロ探索とランダム、原始モンテカルロ探索とアルファ・ベータ法を対戦させて、勝率を表示させるわけですな。
$ python tictactoe.py
0.985
0.365
ほら、ランダムに圧勝で、アルファ・ベータ法に善戦しているでしょ?
モンテカルロ「木」探索
でもね、原始モンテカルロ探索に「原始」なんて枕詞がついているのは、これは古臭いやり方だからなんですよ。当然より良いアルゴリズムがあるわけで、それがモンテカルロ「木」探索です。
平均して良い手が良い手とは限らない
前回のミニ・マックス法でやりましたけど、敵は、敵が有利になる手、私が不利になる手を選びます。10回プレイアウトして9回は勝つけど1回は負ける手があって、もしその1回が必敗の手の場合、いやらしいことに敵はその手を選んできます。つまり、残り9回の勝ちに価値はないわけで、でも、原始モンテカルロ探索だと9/10という高い確率で勝つその悪手を選んでしまいます。
だから、ミニ・マックス法の時みたいに交互に互いが有利な手を選んでいって、それでも勝つ手を選ぶことにしましょう。プレイアウトで勝率を決める、自分に有利な手を選んでその先を読む、プレイアウトで勝率を決める、今度は相手に有利な手を選んでその先を読む……、みたいな感じです。
ただ、合法手は多数あって、その多数の合法手の一つ一つに次の多数の合法手があるので、あっという間に手に負えない数になってしまいます。だから、すべての合法手に一定回数のプレイアウトを実施するような方式は使えません。良い手は深く、悪い手は浅く読むための工夫が必要なわけ。
マルチ・アーム・バンディット問題
この工夫を実現するために、モンテカルロつながりで、カジノのスロット・マシンで考えてみましょう。
「目の前に3台のスロット・マシンがあります。スロット・マシンには、それぞれ異なる勝率が設定されています。でも、その勝率は外からは見えません。さて、それぞれにどれだけのお金を突っ込みますか?」
スロット・マシンの横のガチャコンする棒をアームと呼ぶので、マルチ・アーム・バンディット問題と呼ばれている問題です(ごめんなさい。なんでbandit(山賊)なのかは知りません)。
勝率を調べるためにそれぞれのスロット・マシンで100回ずつモンテカルロ法する……ってのはダメ。無限にお金があるならこれでもよいですけど、そもそも無限にお金があるならカジノには来ません。勝率が低いスロット・マシンに投入するお金は、できるだけ減らしたいですよね。
心に決めた一台に所持金のすべてをつぎ込む。他のスロット・マシンでは勝負しないのだから勝率は分からないわけで、だから私が選んだこの1台より他のスロット・マシンの勝率が高い証拠はない……ってのもダメ。もっと可能性を探らないとね。心情的には分かるけど。
「勝率を探るためにまんべんなく打つ」のと「勝率が高そうなスロット・マシンにつぎ込む」のを、バランス良くやらなければならないんです。これはカジノでだけ通用する話ではなくて、例えばWebアプリケーションのA/Bテストの効率を向上させる場合等にも使える話です。リクエストの半分をページA、残り半分をページBに振り分けて、反応が良かった方のページを選ぶというA/Bテストは、勝率を調べるためにそれぞれのスロット・マシンで100回ずつモンテカルロするってのと同じ程度にダメなやり方なんです。ちなみに、自分が最高だと思うWebページを作ってA/Bテストすらしないってのが、一台に所持金のすべてを突っ込むダメダメな方式です。
では、どうやってバランスを取ればよいのでしょうか? 幸いなことに、偉い人が答を出してくれていました。その答の一つが、UCB1と呼ばれるアルゴリズムです。
UCB1 = (w / n) + (2 * log(t) / n) ** (1 / 2)
# wはこのスロット・マシンの試行回数
# nはこのスロット・マシンの成功回数
# tは総試行回数
なぜ平方根を使わずに1/2乗するのかは私には分かりませんでしたが、(2 * log(t) / n) ** (1 / 2)の部分は、試行回数が少ない場合になんとなく大きな値になるような気はします。この値に勝率である(w / n)を合計した結果が高いスロット・マシンを選んでいけば、なんとなくだけどバランスが取れそうです(私はUCB1の証明をカケラも理解していません……)。マルバツのアクションごとにwとnを用意してあげて、その中からUCB1が最大のものを選んで探索していけば、なんとかなりそう。
そうそう、先程の式は勝ちが1で負けが0の場合用で、勝ちが1で負けが-1になる場合はUCB1 = (w / n) + 2 * (2 * log(t) / n) ** (1 / 2)になります。ちなみに追加された2 *の2は、1 - (-1)の結果。報酬の最大値と最小値の差を掛ければよいらしい。A/Bテストの効率化に使うときは、たとえば課金金額の最大と最小の差を使えばよいのかな。
モンテカルロ木探索
バランスを取る方法がわかりましたから、プログラミングに入りましょう。UCB1が最大になる次のアクションを選んで、プレイアウトする。これを繰り返していくわけですけど、次のアクションをプレイアウトするだけではその先を読めませんから、一定の回数でプレイアウトをやめて、次の次のアクションを選択してプレイアウトするモードに移行します。ただ、モードが変わってもやることは同じ。UCB1が最大になる次の次のアクションを選んで、プレイアウトするだけ。だから、再帰で表現できます。あと、状態の管理が楽になるように、クラスにまとめると良さそう。以上をふまえて作成したのが、以下のnodeクラスです。
class node:
def __init__(self, state):
self.state = state
self.w = 0 # 価値
self.n = 0 # 試行回数
self.child_nodes = None # 子ノード
def evaluate(self):
if self.state.end:
value = -1 if self.state.lose else 0
self.w += value
self.n += 1
return value
if not self.child_nodes:
value = playout(self.state)
self.w += value
self.n += 1
if self.n == 10:
self.expand
return value
else:
value = -self.next_child_node().evaluate()
self.w += value
self.n += 1
return value
def expand(self):
self.child_nodes = tuple(node(self.state.next(action)) for action in self.state.legal_actions)
def next_child_node(self):
def ucb1_values():
t = sum(map(attrgetter('n'), self.child_nodes))
return tuple(-child_node.w / child_node.n + 2 * (2 * log(t) / child_node.n) ** 0.5 for child_node in self.child_nodes)
for child_node in self.child_nodes:
if child_node.n == 0:
return child_node
ucb1_values = ucb1_values()
return self.child_nodes[argmax(ucb1_values)]
evaluate()メソッドが呼ばれると、評価を実施します。if self.state.endの中はゲームが終了している場合の処理です。self.wに負けなら-1、引き分けなら0を足して、self.nをインクリメントします。で、ミニ・マックス方やアルファ・ベータ法のときと同じように、valueをリターンします。
if not self.child_nodesの中は、プレイアウトして勝率(値は-1から1なので率じゃないけど、他の言葉が思いつかない)を設定するモードの処理です。コンストラクタでself.child_nodes = Noneしていますから、最初はこのモードになります。処理は単純で、まずはプレイアウトの結果でゲーム終了の場合と同様にself.wとself.nの値を更新します。で、いつまでもこのモードのままだと先を読むことができませんから、if self.n == 10で、10回プレイアウトしたら子ノードを展開して別モードに移行しています。
elseの中がその別モードで、次の手を評価するモードです。self.next_child_node()でUCB1が最大の子ノードを選んで、再帰呼び出しします。次の手なのでevaluate()の結果の符号を反転させるところだけは注意して、あとはやっぱりこれまでと同じ処理。
next_child_node()メソッドが、上で説明したUCB1が最大の子ノードを選ぶ処理です。一度も評価されていない子ノードのnの値は0で、それだとゼロ除算例外になってしまいますので、for child_node in self.child_nodesの中で、とりあえずすべての子ノードの0が1以上になるようにまんべんなく呼び出しています(すべてのスロット・マシンを最低1回は試さないとね)。child_node.wは敵にとっての価値ですから、符号の反転を忘れないように気をつけてください。
で、プレイアウトで子ノードのwやnの値が変わってくると、バランス良く、しかし、勝率が高い子ノードほど数多く評価されていくことになります。数多く評価された子ノードはif self.n == 10の条件を満たしてさらに子ノードを展開して……となっていきますので、結果として、良さそうな手は深く、そうでない手は浅く読むことになるというわけ。そうそう、先を読んだ結果もwやnにフィードバックされますから、一見良さそうだけど実は相手に有利な手の場合はだんだん評価されなくなります。
あとは、このnodeクラスを使って手を選択する処理を書けば終わり。
def monte_carlo_tree_search_next_action(state):
root_node = node(state)
root_node.expand()
for _ in range(100):
root_node.evaluate()
return state.legal_actions[argmax(root_node.child_nodes, key=attrgetter('n'))]
今の局面のwに意味はありませんから(今の局面が悪くても、前の手をやり直せるわけではない)、いきなりroot_node.expand()してモードを切り替えた上で、100回evaluate()しています。で、最もn(試行回数)が多い手を返す。
どうして最後の最後でw(価値)じゃなくてn(試行回数)を使用するのかというと、試行回数が少ない場合のwは不正確な可能性があるためです。UCB1を使って良さげな手を多数評価したのだから、nは良さを表現する指標として使用できるでしょう。
試してみある
メイン・ルーチンのmonte_carlo_search_next_actionをmonte_carlo_tree_search_next_actionに変更して試してみます。
$ python tictactoe.py
1.0
0.46
はい、原始モンテカルロ探索よりも成績が良くなりました。対アルファ・ベータ法の勝率は最大でも0.5ですから、結構良さそうですね。
せっかく読んだ手が無駄になっているような……
今回の実装では、monte_carlo_tree_search_next_action()が終了すると探索結果をすべて捨てますから、一つ前の手を読んだときと次の手を読むときで、同じノードを複数回評価するかもしれません。これはもったいないのでキャッシュしようぜ……って考えるのは自然なのですけど、そうすると、前の呼び出しで評価済みのノードと今回の呼び出して追加されたノードのnの値がごっちゃになっちゃう。nを親ノードで管理すれば大丈夫な気もしますけど、コードがわかりづらくなりそうです。あと、合流(異なる経路で同じ局面に達する場合)も、マルバツならば多分大丈夫だけど他のゲームでは問題になるような気がします。
あともう少しで最強になれそうだけど、どうにかならないの?
プレイアウトの質を高めれば、更に強くなります。今回のプレイアウトは完全にランダムですけど、たとえばリーチがかかったら阻止するとかの実際に即した形で打つように変更するわけ。これでかなり強くなるはず。あと、評価回数を増やしても強くなります。ただ、マルバツだと終局まで読み切るノードが出てきちゃうので、ほぼミニ・マックス法になっちゃうような気がしますけど……。
それ以外の方法としては、モンテカルロ木探索に深層学習を組み合わせた、Googleのアルファ碁があります。実はすでに実装済みなので、次回はこれを。
最後に、ちょっと試してみたいという場合用に、コード全体を載せておきます。pip3 install funcyして、python3 xxx.pyしてみてください。
from funcy import *
from math import inf, log
from operator import *
from random import randint
def popcount(x):
return bin(x).count('1') # Pythonだと、コレが手軽で速いらしい。
# ゲームの状態。
class State:
def __init__(self, pieces=0, enemy_pieces=0):
self.pieces = pieces
self.enemy_pieces = enemy_pieces
@property
def lose(self):
return any(lambda mask: self.enemy_pieces & mask == mask, (0b111000000, 0b000111000, 0b000000111, 0b100100100, 0b010010010, 0b001001001, 0b100010001, 0b001010100))
@property
def draw(self):
return popcount(self.pieces) + popcount(self.enemy_pieces) == 9
@property
def end(self):
return self.lose or self.draw
@property
def legal_actions(self):
return tuple(i for i in range(9) if not self.pieces & 0b100000000 >> i and not self.enemy_pieces & 0b100000000 >> i)
def next(self, action):
return State(self.enemy_pieces, self.pieces | 0b100000000 >> action)
def __str__(self):
ox = ('o', 'x') if popcount(self.pieces) == popcount(self.enemy_pieces) else ('x', 'o')
return '\n'.join(''.join((ox[0] if self.pieces & 0b100000000 >> i * 3 + j else None) or (ox[1] if self.enemy_pieces & 0b100000000 >> i * 3 + j else None) or '-' for j in range(3)) for i in range(3))
# ランダムで次の手を返します。
def random_next_action(state):
return state.legal_actions[randint(0, len(state.legal_actions) - 1)]
# アルファ・ベータ法(正確にはネガ・アルファ法)
def nega_alpha(state, alpha, beta):
if state.lose:
return -1
if state.draw:
return 0
for action in state.legal_actions:
score = -nega_alpha(state.next(action), -beta, -alpha)
if score > alpha:
alpha = score
if alpha >= beta:
return alpha
return alpha
# 次の手を返します(nega_alphaはスコアを返すので、手を返すようにするためにほぼ同じ関数が必要になっちゃいました)。
def nega_alpha_next_action(state):
alpha = -inf
for action in state.legal_actions:
score = -nega_alpha(state.next(action), -inf, -alpha)
if score > alpha:
best_action = action
alpha = score
return best_action
# プレイアウト。
def playout(state):
if state.lose:
return -1
if state.draw:
return 0
return -playout(state.next(random_next_action(state)))
def argmax(collection, key=None):
return collection.index(max(collection, key=key) if key else max(collection))
# モンテカルロ探索。
def monte_carlo_search_next_action(state):
values = [0] * len(state.legal_actions)
for i, action in enumerate(state.legal_actions):
for _ in range(10):
values[i] += -playout(state.next(action))
return state.legal_actions[argmax(values)]
# モンテカルロ「木」探索。
def monte_carlo_tree_search_next_action(state):
class node:
def __init__(self, state):
self.state = state
self.w = 0 # 価値
self.n = 0 # 試行回数
self.child_nodes = None # 子ノード
def evaluate(self):
if self.state.end:
value = -1 if self.state.lose else 0
self.w += value
self.n += 1
return value
if not self.child_nodes:
value = playout(self.state)
self.w += value
self.n += 1
if self.n == 10:
self.expand
return value
else:
value = -self.next_child_node().evaluate()
self.w += value
self.n += 1
return value
def expand(self):
self.child_nodes = tuple(node(self.state.next(action)) for action in self.state.legal_actions)
def next_child_node(self):
def ucb1_values():
t = sum(map(attrgetter('n'), self.child_nodes))
return tuple(-child_node.w / child_node.n + 2 * (2 * log(t) / child_node.n) ** 0.5 for child_node in self.child_nodes)
for child_node in self.child_nodes:
if child_node.n == 0:
return child_node
ucb1_values = ucb1_values()
return self.child_nodes[argmax(ucb1_values)]
root_node = node(state)
root_node.expand()
for _ in range(100):
root_node.evaluate()
return state.legal_actions[argmax(root_node.child_nodes, key=attrgetter('n'))]
def main():
def first_player_point(ended_state):
if ended_state.lose:
return 1 if (popcount(ended_state.pieces) + popcount(ended_state.enemy_pieces)) % 2 == 1 else 0
return 0.5
def test_algorithm(next_actions):
total_point = 0
for _ in range(100):
state = State()
for next_action in cat(repeat(next_actions)):
if state.end:
break;
state = state.next(next_action(state))
total_point += first_player_point(state)
return total_point / 100
print(test_algorithm((monte_carlo_tree_search_next_action, random_next_action)))
print(test_algorithm((monte_carlo_tree_search_next_action, nega_alpha_next_action)))
if __name__ == '__main__':
main()
2018/06/15
今年49歳になるおっさんでも分かるミニ・マックス法とアルファ・ベータ法
二人零和有限確定完全情報ゲームAIのアルゴリズムといえばとりあえずコレという、ミニ・マックス法とアルファ・ベータ法の説明です。お題はマルバツ、言語はPython3です。
マルバツのルールを実装する
前準備として、マルバツのルールを実装しましょう。いきなりコードでごめんなさい。
from funcy import *
def _popcount(x):
return bin(x).count('1') # Pythonだと、コレが手軽で速いらしい。
# ゲームの状態。
class State:
def __init__(self, pieces=0, enemy_pieces=0):
self.pieces = pieces
self.enemy_pieces = enemy_pieces
@property
def lose(self):
return any(lambda mask: self.enemy_pieces & mask == mask, (0b111000000, 0b000111000, 0b000000111, 0b100100100, 0b010010010, 0b001001001, 0b100010001, 0b001010100))
@property
def draw(self):
return _popcount(self.pieces) + _popcount(self.enemy_pieces) == 9
@property
def end(self):
return self.lose or self.draw
@property
def legal_actions(self):
return tuple(i for i in range(9) if not self.pieces & 0b100000000 >> i and not self.enemy_pieces & 0b100000000 >> i)
def next(self, action):
return State(self.enemy_pieces, self.pieces | 0b100000000 >> action)
def __str__(self):
ox = ('o', 'x') if _popcount(self.pieces) == _popcount(self.enemy_pieces) else ('x', 'o')
return '\n'.join(''.join((ox[0] if self.pieces & 0b100000000 >> i * 3 + j else None) or (ox[1] if self.enemy_pieces & 0b100000000 >> i * 3 + j else None) or '-' for j in range(3)) for i in range(3))
盤面はビット・フィールドで表現しています。0b100000000だと左上にマルやバツが書き込まれた状態、0b000010000なら真ん中です。piecesが自分のビット・フィールドでenemy_piecesが敵のビット・フィールド。次の盤面を求めるnextで、piecesとenemy_piecesを入れ替えます。loseは負けかどうか、drawは引き分けかどうか、endはゲーム終了かどうか、legal_actionsは合法手の一覧を返します。あと、from funcy import *の「funcy」は、私が愛用しているPython用の関数型プログラミングのライブラリです。とても役立つライブラリなので、pip install funcyしてみてください。
でね、このコードはミニ・マックス法ともアルファ・ベータ法とも関係はありませんので、お前はマルバツのルールはこんな感じに実装したのねー程度で見ていただければオッケーです。ビット・フィールドの表現をちょっと頑張ったので見て欲しかっただけという……。
とりあえず、ランダムで手を選んでゲームをさせる
ともあれ、ルールができたので、ゲームをさせてみましょう。
まずは、ランダムで手を選択するマルバツAIです。合法手の一覧を実装済みですから、必要なコードはこれだけ。
from random import randint
def random_next_action(state):
return state.legal_actions[randint(0, len(state.legal_actions) - 1)]
このAI同士でゲームをさせてみましょう。コードはこんな感じ。
def main():
state = State()
white True:
if state.end:
break;
state = state.next(random_next_action(state))
print(state)
print()
if __name__ == '__main__':
main()
動かしてみると、たしかにランダムに手を打って勝ったり負けたりしています。馬鹿と阿呆がゲームしている感じ。
$ python tictactoe.py
o--
---
---
o--
x--
---
o--
x--
-o-
o--
x-x
-o-
o-o
x-x
-o-
o-o
x-x
-ox
o-o
x-x
oox
o-o
xxx
oox
ミニ・マックス法
馬鹿と阿呆のゲームでは面白くないので、ミニ・マックス法を駆使して絶対に負けないマルバツAIを作りましょう。
先を読む
一般にゲームでは、私がここに打ったら、相手がここに打って、そうなると次に私はここに打って……という感じに先を読んでいきます。ただし、私が打てる手は複数あり、敵が打てる手も複数あって、だからほんの少し読むだけで莫大な数の盤面が出てきてしまいます。人間にはこの多数の盤面を列挙するのは辛いですけど、コンピューターなら余裕(時間はかかりますけど)。というわけで、すべての状態を表示するコードを作成してみました。
def foo(state):
print(state)
print()
for action in state.legal_actions:
foo(state.next(action))
で、こんな感じに先を読めるとして、で、どの手を選べば良いのでしょうか?
私が勝つ盤面へと進む手を、相手は選ばない。相手は、私が負ける盤面に進む手を選ぶ
まず思いつくのは、先読みして私が勝つ状態を1つ見つけたら、そのルートに入る手を選択するという方法です。でも、この方法はうまく行きません。
考えてみましょう。私がマルだとして、以下の勝ち盤面を見つけたとします。
ooo
xx-
---
この一つ前の状態が以下だとしましょう。
oo-
xx-
---
そのもう一つ前の状態は以下のような感じ。
oo-
x--
---
ここでマルの勝利を目指して真ん中にバツを打ってくれる相手はいませんよね? 右上にバツを打って、マルの勝利を邪魔するはずです。つまり、私は私が勝つ盤面へと進む手を選びますけど、相手は私が「負ける」盤面へと進む手を選ぶのです。
勝敗を数値で表現する
私が勝つとか負けるとかだと少しふわふわしていますから、コードで扱いやすい数値で表現することにしましょう。こんな感じ。
if state.lose: # 負けちゃったら、
return -1 # 評価はマイナスですよね。
if state.draw: # 引き分けになったら、
return 0 # 負けよりはマシなゼロ。
上のコードに勝ちがないのは、私が負ける盤面は相手にとっての勝ちだからです。負けである-1を勝ちである1に変換するには、-(マイナス)をつけてあげればオッケー(-0は0なので引き分けは影響を受けません)。以下のような感じでしょうか?
def foo(state):
if state.lose:
return -1
if state.draw:
return 0
for action in state.legal_actions:
score = -foo(state.next(action)) # このscoreが大きいのが、良い盤面
...
負けでも引き分けでもなければ再帰呼び出しして、-をつけて自分のスコアにしちゃうわけです。
ooo
xx-
---
は負けなので-1になって、だからその前の
oo-
xx-
---
で右上にマルを打った場合のスコアは-(-1)で「1」になるというわけ。このやり方はスコアの符号を入れ替えながら何回でも続けることができて、だから、最初の一手を打つ場合にも同じ考え方でいけます。
というわけで、自分も相手も最善を尽くす場合の、盤面のスコアを出す関数は、以下になります。
from math import inf
def score(state):
if state.lose:
return -1
if state.draw:
return 0
best_score = -inf
for action in state.legal_actions:
score = -foo(state.next(action))
if score > best_score:
bext_score = score
return best_score
ミニ・マックス法
で、実は先程のコードはミニ・マックス法(正確にはネガ・マックス法)そのものなんです。相手はスコアが最小のものを、自分はスコアが最大の盤面を選ぶのがミニ・マックス法。今回は符号を反転しているので毎回最大のスコアを選べば良くて、この方式はネガ・マックス法と呼ばれています。だから、名前を変えましょう。あと、我々が欲しいのはどの手を選択すればよいかで、盤面のスコアではありませんから、手を選択する関数も追加しました。
from math import inf
# ミニ・マックス法(正確にはネガ・マックス法)
def nega_max(state):
if state.lose:
return -1
if state.draw:
return 0
best_score = -inf
for action in state.legal_actions:
score = -nega_max(state.next(action))
if score > best_score:
best_score = score
return best_score
# 次の手を返します(nega_maxはスコアを返すので、手を返すようにするためにほぼ同じ関数が必要になっちゃいました)。
def nega_max_next_action(state):
best_score = -inf
for action in state.legal_actions:
score = -nega_max(state.next(action))
if score > best_score:
best_action = action
best_score = score
return best_action
試してみましょう。メイン・ルーチンを以下に変えます。
def main():
state = State()
for next_action in cat(repeat((random_next_action, nega_max_next_action))):
if state.end:
break;
state = state.next(next_action(state))
print(state)
print()
cat(repeat((random_next_action, nega_max_next_action)))で(random_next_action, nega_max_next_action, random_next_action, nega_max_next_action...)と無限に続く集合作成して、順に使用しています。
$ python tictactoe.py
---
--o
---
--x
--o
---
--x
--o
-o-
x-x
--o
-o-
x-x
-oo
-o-
xxx
-oo
-o-
後手のnega_max_next_actionが勝ちました。たまに引き分けはありますけど、絶対に負けはしません。これでミッション・コンプリート?
アルファ・ベータ法
いいえ。まだミッションは完了してません。というのも、nega_max_next_actionに先手をやらせると、初手を打つまでにやたらと長い時間がかかるってしまうんですよ。アルファ・ベータ法を駆使して読む範囲を減らして、高速なマルバツAIを作りましょう。
枝狩りとは?
まぁ、すべてののありえる局面を読んでいたら時間がかかるのは当然で、だから読む範囲を減らせば良いわけです。次の手、その次の手、さらにその次の手と読んでいくと選択肢が木構造になっていって、ある選択肢を読まないことは木の枝を捨てることに相当するので、「枝狩り」と呼びます。
マルバツですぐに思いつく枝狩りの対象は、盤面を反転させたり回転させたりしたケースです。初手が左上の場合を読んだら、右上とか右下とか左下の場合はその回転なのだから読む必要はないですよね? マルバツをやっている途中で盤面を90度変えたら結果が変わったなんて話は聞かないですもんね。ただ、ごめんなさい。この枝狩りは今回は作成していません。もしこれをやってミニ・マックス法でも十分な速度が出ちゃったら、アルファ・ベータ法をやる理由がなくなっちゃいますから。
というわけで、今回は作成したのは、スコアの範囲に着目した枝狩りであるアルファ・ベータ法です。
もし勝つ手があるなら、負ける手は選ばない。相手も同様だけど、相手の勝ちは私の負けなので、相手が選ぶ相手の勝ちは選ばれない
先程のコードのnega_max_next_actionで、1つ目のactionのスコアが「0」(引き分け)と出た場合を考えてください。2つ目以降のactionで選ばれる可能性があるのは、スコアが0を超える場合、スコアが「1」(勝ち)の場合だけですよね? もし2つめのactionのスコアが「-1」(負け)なら、それを選ぶのは馬鹿げています。そして「0」なら、わざわざ手を変える必要はありません。
これを相手(-nega_max(state.next(action))で呼ばれた先)の立場で考えてみると、もし「1」(勝ち)や「0」(引き分け)のアクションがあっても、それは選んでもらえないことになります(思い出してください。相手の勝ちは自分の負けなので、「1」は「-1」になります)。
そして、相手(-nega_max(state.next(action))で呼ばれた先)もやっぱり最大のスコアを選びたいわけなので、もし1つ目のアクションが「0」(引き分け)なら、「-1」(負け)は選びません。「1」(勝ち)なら選ぶかもしれませんけど、「0」でも「1」でも、呼び出し元に選んでもらえない無駄な値という意味では同じです。
つまり、-best_score以上の値が出たら、その先を読んでも無駄なんです(-best_score以上の値が出た読みそのものも無駄なのですけど、これをやらないと無駄かどうかがわからないのでしょうがない)。というわけで、こんな感じでどうでしょうか?
def foo(state, limit):
if state.lose:
return -1
if state.draw:
return 0
best_score = -inf
for action in state.legal_actions:
score = -foo(state.next(action), -best_score)
if score > best_score:
best_score = score
if best_score >= limit:
return best_score # どうせ選ばれないんだから、このスコアは無効という意味でinfとかを返しても構いません。
return best_score
試してみると、おお、すげー速い。
敵の敵は味方、じゃなくて自分
でも、さらに効率化できるんですよ。-foo()の先で呼びだされる-foo()は自分自身(敵の敵は自分)ですよね? もしそこでbest_score以下のスコアが出ても、if score > best_scoreで無視されちゃうわけです。だから、2つ先の呼び出しのbest_scoreを-infではなく今のbest_scoreから始めても大丈夫なわけ。で、best_scoreの初期値が大きければ、その先の呼び出しで枝狩りできる範囲が広がる効果も期待できちゃう。
というわけで、変数を2つ用意しましょう。alphaとbetaです。コードは以下の通り。
from math import inf
# アルファ・ベータ法(正確にはネガ・アルファ法)
def nega_alpha(state, alpha, beta):
if state.lose:
return -1
if state.draw:
return 0
for action in state.legal_actions:
score = -nega_alpha(state.next(action), -beta, -alpha)
if score > alpha:
alpha = score
if alpha >= beta:
return alpha
return alpha
# 次の手を返します(nega_alphaはスコアを返すので、手を返すようにするためにほぼ同じ関数が必要になっちゃいました)。
def nega_alpha_next_action(state):
alpha = -inf
for action in state.legal_actions:
score = -nega_alpha(state.next(action), -inf, -alpha)
if score > alpha:
best_action = action
alpha = score
return best_action
best_scoreがalphaになっただけです。これでアルファ・ベータ法(正確にはネガ・アルファ法)は完成。試してみましょう。
def main():
state = State()
for next_action in cat(repeat((nega_alpha_next_action, nega_max_next_action))):
if state.end:
break;
state = state.next(next_action(state))
print(state)
print()
実行結果は以下の通り。
$ python tictactoe.py
o--
---
---
o--
-x-
---
oo-
-x-
---
oox
-x-
---
oox
-x-
o--
oox
xx-
o--
oox
xxo
o--
oox
xxo
ox-
oox
xxo
oxo
絶対に負けないAI同士が対戦して、結果は引き分けになっています。初手も速いですし、はい、これで完成です。
最後まで読めない複雑なゲームはどうするの?
でも、世の中にはマルバツよりも複雑なゲームがあって、複雑なゲームでは最後まで読み切ることはできません。ではどうするかというと、一定の深さまでしか読まないことにして、その深さの盤面のスコアを勝敗とは別の要因で決めるんです。例えばオセロならいい場所に自分のコマがあるかどうかで、将棋ならばどのようなコマを持っているかとか自分のコマと相手の玉の位置関係とかで。このように盤面を評価してスコアを無理やり出す関数を評価関数と呼ぶのですけど、強い評価関数を作るのは難しくて今年49歳になるおっさんでは説明できませんでした。ごめんなさい……。
最後に、ちょっと試してみたいという場合用に、コード全体を載せておきます。pip3 install funcyして、python3 xxx.pyしてみてください。
from funcy import *
from math import inf
from random import randint
def _popcount(x):
return bin(x).count('1') # Pythonだと、コレが手軽で速いらしい。
# ゲームの状態。
class State:
def __init__(self, pieces=0, enemy_pieces=0):
self.pieces = pieces
self.enemy_pieces = enemy_pieces
@property
def lose(self):
return any(lambda mask: self.enemy_pieces & mask == mask, (0b111000000, 0b000111000, 0b000000111, 0b100100100, 0b010010010, 0b001001001, 0b100010001, 0b001010100))
@property
def draw(self):
return _popcount(self.pieces) + _popcount(self.enemy_pieces) == 9
@property
def end(self):
return self.lose or self.draw
@property
def legal_actions(self):
return tuple(i for i in range(9) if not self.pieces & 0b100000000 >> i and not self.enemy_pieces & 0b100000000 >> i)
def next(self, action):
return State(self.enemy_pieces, self.pieces | 0b100000000 >> action)
def __str__(self):
ox = ('o', 'x') if _popcount(self.pieces) == _popcount(self.enemy_pieces) else ('x', 'o')
return '\n'.join(''.join((ox[0] if self.pieces & 0b100000000 >> i * 3 + j else None) or (ox[1] if self.enemy_pieces & 0b100000000 >> i * 3 + j else None) or '-' for j in range(3)) for i in range(3))
# ランダムで次の手を返します。
def random_next_action(state):
return state.legal_actions[randint(0, len(state.legal_actions) - 1)]
# ミニ・マックス法(正確にはネガ・マックス法)
def nega_max(state):
if state.lose:
return -1
if state.draw:
return 0
best_score = -inf
for action in state.legal_actions:
score = -nega_max(state.next(action))
if score > best_score:
best_score = score
return best_score
# 次の手を返します(nega_maxはスコアを返すので、手を返すようにするためにほぼ同じ関数が必要になっちゃいました)。
def nega_max_next_action(state):
best_score = -inf
for action in state.legal_actions:
score = -nega_max(state.next(action))
if score > best_score:
best_action = action
best_score = score
return best_action
# アルファ・ベータ法(正確にはネガ・アルファ法)
def nega_alpha(state, alpha, beta):
if state.lose:
return -1
if state.draw:
return 0
for action in state.legal_actions:
score = -nega_alpha(state.next(action), -beta, -alpha)
if score > alpha:
alpha = score
if alpha >= beta:
return alpha
return alpha
# 次の手を返します(nega_alphaはスコアを返すので、手を返すようにするためにほぼ同じ関数が必要になっちゃいました)。
def nega_alpha_next_action(state):
alpha = -inf
for action in state.legal_actions:
score = -nega_alpha(state.next(action), -inf, -alpha)
if score > alpha:
best_action = action
alpha = score
return best_action
def main():
state = State()
for next_action in cat(repeat((nega_alpha_next_action, nega_max_next_action))): # random_next_action, nega_max_next_action, nega_alpha_next_actionの中から適当に選んでください
if state.end:
break;
state = state.next(next_action(state))
print(state)
print()
if __name__ == '__main__':
main()