2018/02/03
深層学習でダメ絶対音感を作ってみた
この前、Amazonプライム・ビデオで「がっこうぐらし!」を見たんですけど、主人公のゆきの声が「けいおん」の唯の声の豊崎愛生さんに聞こえてしまって、そういえば豊崎愛生さん結婚しちゃったんだよなぁと感傷にふけっていたら、ゆきのCVは水瀬いのりさんでした……。
あれ? 年を取ってモスキート音が聞こえなくなっただけじゃなくて、ダメ絶対音感も衰えてる?
老眼は遠近両用メガネで対応できたのですけど、ダメ絶対音感対策デバイスはAmazonでも見つかりません。しょうがないので、自分で作りました。
#ダメ「相対」音感くらいはできたかなぁと。あ、タマキじゃなくてキマリだった……。
データ集め
まずは、適当に選んだ以下のビデオの音声を録音しました。
- Re:ゼロから始める異世界生活(5話)
- がっこうぐらし!(5話)
- この素晴らしい世界に祝福を!2(2話)
- ゆるキャン△(2話)
- カウボーイビバップ(1話)
- 宇宙よりも遠い場所(2話)
- 映画「けいおん!」
録画した音声を、ツール(私が使用したのはAudacity)を使用して0.2秒の無音部分で分割していきます。
分割した音声ファイルを1つずつ聞いて、うまいことキャラクター単位に分かれたファイルだけを抽出して、キャラクター単位に分けます(深層学習が音楽を消すフィルターを作って人間の声の特徴だけを抽出してくれることを期待して、後ろで音楽が流れていても気にしない)。
キャクター単位で音声ファイルを結合して0.5秒単位で分割して、音声のままだとデータが大きすぎて大変そうだったので、MFCC(メル周波数ケプストラム係数)で44×44のデータに変換して、教師データとします。データ件数は、8,349件になりました。
注意!
実は私、音声は素人です。あと、深層学習も趣味レベルです。ただのプログラミング好きなおっさんなんですよ……。
さっきはさらっとMFCCとか書いちゃいましたけど、MFCCが具体的にどんなことをしているのか全く理解していません。プロが見たらおかしなことをやっていると思いますので、ご指摘してくださるようお願いいたします。
学習
音声は持続性があるデータなので、本当は再帰型のニューラル・ネットワークを使ったほうが良い気がしますけど、使い慣れた畳み込みニューラル・ネットワークで押し通しました(0.5秒で分割しちゃったし)。その畳込みニューラル・ネットワークも借り物で、WideResNetを使用しました。コードは、以下のような感じ。Kerasを使うと、私のような素人でも簡単に深層学習できますな。
import pickle
from data_set import load_data # データ読み込み
from funcy import identity, juxt, partial, rcompose, repeatedly # 関数型プログラミング・ライブラリ。便利!
from keras.callbacks import ReduceLROnPlateau
from keras.layers import Activation, Add, AveragePooling2D, BatchNormalization, Conv2D, Dense, GlobalAveragePooling2D, Input
from keras.models import Model, save_model
from keras.optimizers import Adam
from keras.regularizers import l2
from utility import ZeroPadding # ゼロ詰めしたテンソルで次元数を増やすユーティリティ。
def computational_graph(class_size):
# Kerasはシーケンスが嫌いみたいなので、リスト化するバージョンのjuxtを作っておきます。
def ljuxt(*fs):
return rcompose(juxt(*fs), list)
# 以下、Kerasのラッパーです。
def add():
return Add()
def average_pooling():
return AveragePooling2D()
def batch_normalization():
return BatchNormalization()
def conv(filters, kernel_size):
return Conv2D(filters, kernel_size, padding='same', kernel_initializer='he_normal',
kernel_regularizer=l2(0.0001), use_bias=False)
def dense(units):
return Dense(units, kernel_regularizer=l2(0.0001))
def global_average_pooling():
return GlobalAveragePooling2D()
def relu():
return Activation('relu')
def softmax():
return Activation('softmax')
def zero_padding(filter_size):
return ZeroPadding(filter_size)
# WideResNetの計算グラフ。
def wide_residual_net():
def residual_unit(filter_size):
return rcompose(ljuxt(rcompose(batch_normalization(),
conv(filter_size, 3),
batch_normalization(),
relu(),
conv(filter_size, 3),
batch_normalization()),
identity),
add())
def residual_block(filter_size, unit_size):
return rcompose(zero_padding(filter_size),
rcompose(*repeatedly(partial(residual_unit, filter_size), unit_size)))
return rcompose(conv(16, 3),
residual_block(160, 4),
average_pooling(), # 個人的な好みで、ストライドではなくて平均プーリング。
residual_block(320, 4),
average_pooling(),
residual_block(640, 4),
global_average_pooling())
# 計算グラフを返します。WideResNetの出力を、全結合層で256次元→32次元と段階的に小さくして、ソフトマックスします。
return rcompose(wide_residual_net(),
dense(256),
dense(class_size),
softmax())
def main():
# 教師データを読み込みます。
(x_train, y_train), (x_validate, y_validate) = load_data()
# 正規化のためのパラメーター。
x_mean = -14.631151332833856 # x_train.mean()
x_std = 92.12358373202312 # x_train.std()
# xを正規化して、Kerasのconvが通るように[?, 44, 44, 1]に形を変えます。
x_train, x_validate = map(lambda x: ((x - x_mean) / x_std).reshape(x.shape + (1,)), (x_train, x_validate))
# yのデータは[?, 2(0が声優で1がキャラクター)]になっているので、キャラクター部分だけを取ります。
y_train, y_validate = map(lambda y: y[:, 1], (y_train, y_validate))
# モデルを生成します。
model = Model(*juxt(identity, computational_graph(max(y_validate) + 1))(Input(shape=x_validate.shape[1:])))
model.compile(loss='sparse_categorical_crossentropy', optimizer=Adam(lr=0.0005), metrics=['accuracy'])
model.summary()
# 学習します。バッチ・サイスは100、エポック数はとりあえず大きく400にしてみます。GPUのメモリが少ない場合は、バッチ・サイズを減らしてみてください。
results = model.fit(x_train, y_train, batch_size=100, epochs=400,
validation_data=(x_validate, y_validate),
callbacks=[ReduceLROnPlateau(factor=0.5, patience=20, verbose=1)])
# 学習履歴を保存します。
with open('./results/history.pickle', 'wb') as f:
pickle.dump(results.history, f)
# モデルを保存します。
save_model(model, './results/model.h5')
# 必要か分からないけど、モデルを破棄します。
del model
if __name__ == '__main__':
main()
学習の結果、適当により分けておいた検証データでの精度が80%を超えました。これならダメ絶対音感も実現できそうです。
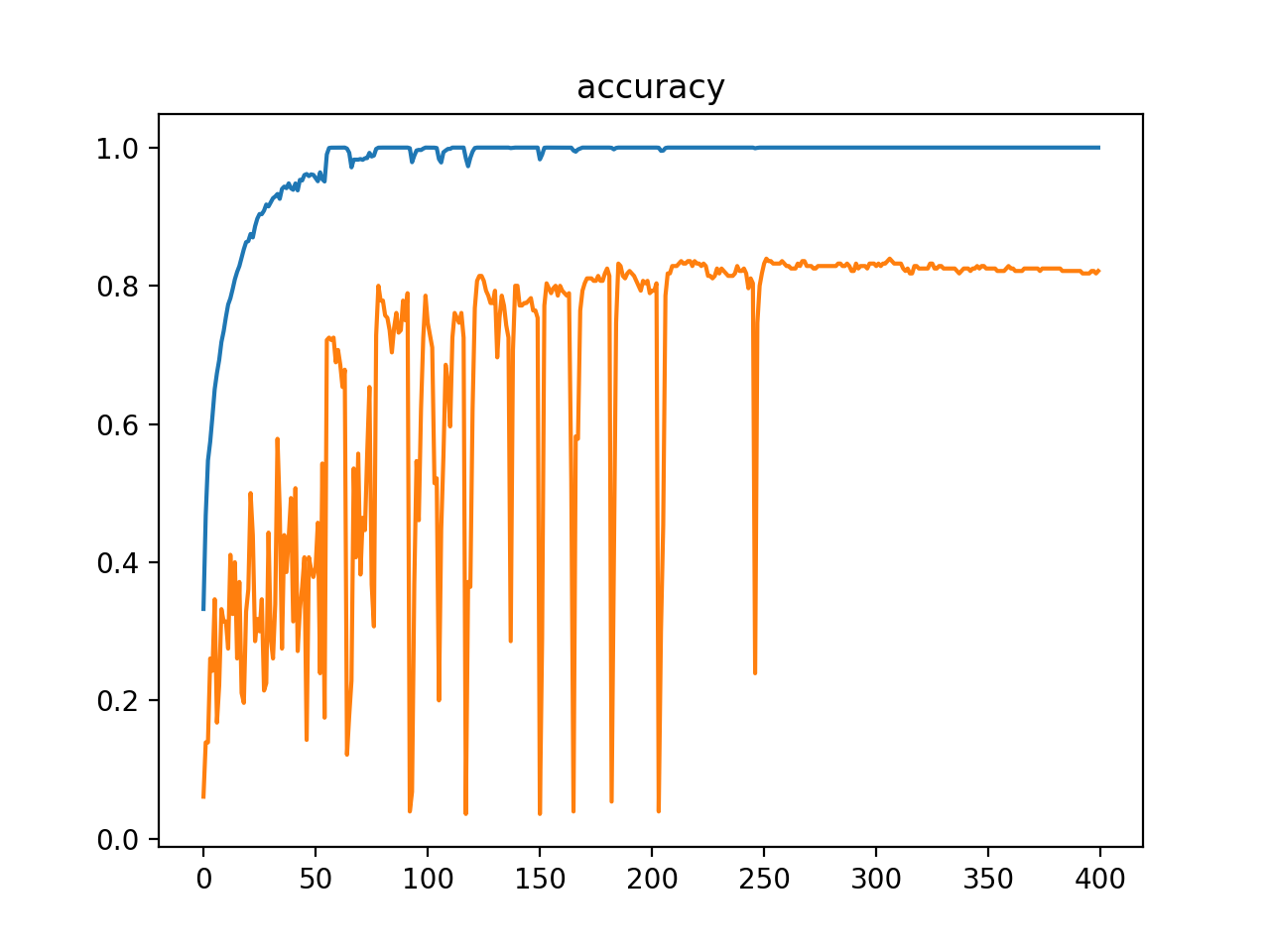
#エポック数は300くらいが良かったかも……。
ダメ絶対音感
録音はPyAudioで、MFCC化はlibrosaで実施しました。とても楽ちんです。
import librosa
import numpy as np
import os.path as path
import pyaudio
import tensorflow as tf
from funcy import first, second
from keras.models import load_model
from useless_absolute_pitch_frame import UselessAbsolutePitchFrame
from utility import ZeroPadding, child_paths
# キャラクター・データのパスを取得します(キャラクター・データのパスに画像データが入っているため)。
def character_paths():
for actor_path in filter(path.isdir, child_paths('./data/validate')):
for character_path in filter(path.isdir, child_paths(actor_path)):
yield character_path
# メイン・ルーチン。
def main():
# PyAudioのコールバック。
def stream_callback(data, frame_count, time_info, status):
# コールバックは別スレッドになるので、使用するグラフを指定しないとTensorFlowが動きませんでした。
with graph.as_default():
# 音声データをNumPy化します。
wave = np.frombuffer(data, dtype=np.float32)
# MFCC化します。n_mfccが44なのは、0.5秒だと横方向が44になったためです。
mfcc = librosa.feature.mfcc(wave, sr=44100, n_mfcc=44)
# 正規化し、モデル作成時のInputと同じなるように[?, 44, 44, 1]に形を変えてxにします。
x = ((mfcc - -14.631151332833856) / 92.12358373202312).reshape((1,) + mfcc.shape + (1,))
# キャラクターを推論します。
y = model.predict(x)
# 後述するGUIに表示するように命令します。
gui.draw_predict_result(wave, tuple(map(second, reversed(sorted(zip(y[0], range(len(y[0]))), key=first)))))
# 続けて処理するよう、PyAudioに指示します。
return data, pyaudio.paContinue
# PyAudio。便利!
audio = pyaudio.PyAudio()
# モデルの読み込み。PyAudioのコールバックが別スレッドなので、TensorFlowの計算グラフを保存しておきます。
model = load_model('./results/model.h5', custom_objects={'ZeroPadding': ZeroPadding})
graph = tf.get_default_graph()
# PyAudio経由で録音。
stream = audio.open(format=pyaudio.paFloat32, channels=1, rate=44100, input=True,
frames_per_buffer=22050, stream_callback=stream_callback)
stream.start_stream()
# 後述するGUIを生成。
gui = UselessAbsolutePitchFrame(tuple(character_paths()))
gui.mainloop()
# 終了処理。
stream.stop_stream()
stream.close()
audio.terminate()
if __name__ == '__main__':
main()
GUI部分はtkinterで作りました。tkinterが使いづらくて、ここに一番時間がかかりました……。コードが汚いですけど、リファクタリングはまた今度で。
import numpy as np
import os.path as path
from funcy import count, juxt, map
from tkinter import *
from tkinter.ttk import *
class UselessAbsolutePitchFrame(Frame):
def __init__(self, character_paths, master=None):
super().__init__(master)
# キャラクターの画像を取得。tkinterのPhotoImageって、GIFかPPMじゃないとダメだと知らなくて、ひどい目にあいました。
self.character_images = tuple(map(lambda character_path: PhotoImage(file=path.join(character_path, 'image.ppm')), character_paths))
self.character_small_images = tuple(map(lambda character_path: PhotoImage(file=path.join(character_path, 'small_image.ppm')), character_paths))
# GUIを生成します。
self.master.title('ダメ絶対(?)音感')
self.create_widgets()
self.pack()
# GUIを生成します。
def create_widgets(self):
frame_1 = Frame(self)
# 音声の波形を表示するためのキャンバス。
self.wave_canvas = Canvas(frame_1, width=256, height=256)
self.wave_canvas.grid(row=0, column=0)
# 推論したキャラクターを表示するためのキャンバス。
self.character_canvas = Canvas(frame_1, width=256, height=256)
self.character_canvas.grid(row=0, column=1)
frame_1.pack()
frame_2 = Frame(self)
# 推論結果の確率が高い順に、キャラクターをソートして表示するためのキャンバス。
self.characters_canvas = Canvas(frame_2, width=512, height=64)
self.characters_canvas.pack()
frame_2.pack()
# 推論結果を表示します。
def draw_predict_result(self, wave, character_indice):
self.draw_wave(wave)
self.draw_predicted_character(character_indice[0])
self.draw_predicted_characters(character_indice)
self.update()
# 音声の波形を表示します。
def draw_wave(self, wave):
min_ys, max_ys = zip(*map(juxt(np.min, np.max), np.array_split(wave * 128 + 128, 256)))
for object_id in self.wave_canvas.find_all():
self.wave_canvas.delete(object_id)
for x, min_y, max_y in zip(count(), min_ys, max_ys):
self.wave_canvas.create_line(x, min_y, x, max_y)
# 推論したキャラクターを表示します。
def draw_predicted_character(self, character_index):
for object_id in self.character_canvas.find_all():
self.character_canvas.delete(object_id)
self.character_canvas.create_image(128, 128, image=self.character_images[character_index])
# 推論結果の確率でソートして、可能性が高い順にキャラクターを表示します。
def draw_predicted_characters(self, character_indice):
for object_id in self.characters_canvas.find_all():
self.characters_canvas.delete(object_id)
for i in range(8):
self.characters_canvas.create_image(i * 64 + 32, 32, image=self.character_small_images[character_indice[i]])
ともあれ、これで完成! 録音したのとは異なる話数のビデオをAmazonプライム・ビデオで流しながら試してみたら、冒頭のアニメーションGIF(まぁ、これはいくつか試した中で良かった場合の例なのですけど。あと、ダメ絶対音感の方を0.5秒すすめるかたちで編集しています)で示したみたいにそれなりの精度で判定をしてくれるんだけど、誰も喋っていないところ(左上の音声の波形が小さい時)でガチャガチャ推測結果が変わって落ち着きません。
人が喋っているのかいないのかを判断する技術が必要……なんですけど、素人なのでその方法が思いつきません。誰か助けてください……。このままだと、ゆるふわ系主人公のアニメを見るたびに、豊崎愛生さん結婚ショックがぶり返しちゃう!
参考
音楽と機械学習 前処理編 MFCC ~ メル周波数ケプストラム係数 ←MFCCはここで知りました。最初のコードの部分以外は、全く理解できませんでしたが……。
devil-ear ←本稿で作成したコードです。
2018/02/01
JavaScript(ES6)とRamdaで関数型プログラミング
さっき「関数型プログラミング」でGoogle検索したら最初に表示された「関数型プログラミングはまず考え方から理解しよう」というページ、本文はもちろん、活発な議論がなされたコメント部分も、とても面白かったです。
ただ、コメント中のHaskellの美しいコードは、無限リストが使えるからこその書き方なんですよね……。このやり方は、JavaScriptだとちょっと辛い。コメント中でHaskellと同様のやり方をJavaScriptで書いてくださっている方も、繰り返す数を指定することで対処しています。
うんやっぱりHaskellはすげーなぁというのは当然なんだけど、JavaScriptを気に入っている私としては、実はJavaScriptもそれなりにすごいんだよということを示しておきたい。だから、JavaScript(EcmaScript 6)に関数型プログラミング向けライブラリのRamdaをインポートして、同じお題でプログラミングしてみました。
元ページのお題
詳しくは元ページを見ていただくとして、簡単に書くとこんな感じ。
- 唐揚げ弁当がいくつかあります。唐揚げを何個か、つまみ食いしたいです。
- バレづらいように、最も唐揚げの数が多い弁当からつまみ食いしましょう。
とりあえず、関数型で書いてみた
#後で述べますけど、このコードはかなりヘッポコです……。後で修正しますから、ここで見捨てないで。
というわけで、とりあえず関数型プログラミングした結果は以下の通り。
// ES6なのでrequireじゃなくてimport。
import R from 'ramda';
// 元ネタから、データ構造をちょっと変更。
const lunchBoxes = [{'唐揚げ': {count: 10}, '玉子焼き': {count: 1}},
{'唐揚げ': {count: 8}},
{'唐揚げ': {count: 6}}];
// つまみ食い。
function eatWithFinger(foodName, lunchBoxes) {
// foodNameの数量が最大の弁当のインデックスを取得します。
const canEatIndex = R.apply(R.reduce(R.maxBy(([lunchBox, i]) => lunchBox[foodName].count)),
R.juxt([R.head, R.tail])(R.addIndex(R.map)(R.constructor(Array), lunchBoxes)))[1];
// canEatIndexの弁当のfoodNameの数量を1減らした、新しいリストを返します。
return R.assocPath([canEatIndex, foodName, 'count'], lunchBoxes[canEatIndex][foodName].count - 1, lunchBoxes);
}
export default function main() {
// 唐揚げを5回つまみ食い。
const eatKaraageWithFingerFiveTimes = R.apply(R.pipe)(R.repeat(R.curry(eatWithFinger)('唐揚げ'), 5));
console.log(eatKaraageWithFingerFiveTimes(lunchBoxes));
}
// [10, 8, 6] → [9, 8, 6] → [8, 8, 6] → [7, 8, 6] → [7, 7, 6] → [6, 7, 6]となるので、
// 各弁当の唐揚げの数は、6個、7個、6個になります。
以下、Ramdaの使い方の解説です。Ramdaをご存知の方は飛ばしてください。
R.applyは、f(a, b, c)という関数を[a, b, c]という引数で呼び出せるように変換する関数です。で、Ramdaが提供する関数はすべてカリー化されていて、だからR.apply(f)とやると[a, b, c]を引数にとる関数が返ってきます(R.apply(f(a))なら、[b, c]が引数になる)。で、上のコードでR.reduceをR.applyしているのは、R.reduceの引数はR.reduce(f, initialValue, xs)となっていて、初期値(initialValue)を必ず指定しなければならないためです(JavaScriptのArrayのreduceでは、初期値を指定しない場合は自動でArrayの最初の要素が初期値になるのに……)。
でR.maxByは、R.maxBy(pred, x, y)とするとpred(x)とpred(y)を比較して、大きな方(xかy)を返す関数です。これも当然カリー化されているので、R.maxBy(pred)すると引数を2個とる関数が返されて、それはR.reduceの第一引数の関数にちょうどよいというわけ。なので、上のコードではR.reduce(R.maxBy())して最大の要素を求めています。
R.juxtは、複数の関数に同じ引数を渡すための処理です。R.juxt([foo, bar])(x)とすると[foo(x), bar(x)]が返ってきます。R.headは最初の要素、R.tailは二番目から最後までのリストを返すので、これでやっとR.reduceの引数が揃います。
で、そのR.juxtした関数に渡しているのは、R.addIndex(R.map)(R.constructor(Array))したlunchBoxesです。R.addIndexはインデックス対応バージョンの関数を返しますので、これで[[lunchBox[0], 0], [lunchBox[1], 1] ...]が手に入るというわけ。あ、R.constructorは、扱いが面倒なコンストラクタを関数化する関数です。あと、[lunchBox, index]のうち、canEatIndexとして表現したいのはindexの方なので、最後に[1]を追加しています。
あとは、R.assocPathで、lunchBoxesを修正した新しいlunchBoxesを返すだけ。この関数をR.curryでカリー化して、R.repeatで5個並べて、R.pipeで順に呼び出すようにしています(R.pipe(a, b, c)(x)とするとc(b(a(x)))になります。aしてbしてcするのを順序どおりに表現できるので、私はこの関数が大好きです)。
これで、繰り返し回数をつまみ食いする関数から分離できました(R.repeatの引数に移動しただけという気もしますが……)。元ページみたいにつまみ食いした途中のlunchBoxesを取得したい場合は、R.tapするとか(デバッグのときに便利です)、R.pipeじゃなくてR.reduceするとかで大丈夫かと。
以上、Ramdaの解説終わり。ふう、これで関数型プログラミングのコードができあがりました。
念のため、手続き型で書いてみた
でも、関数型プログラミングのコードだけあっても、良いか悪いか判断できませんよね? 異なる手法でプログラミングしたコードと比較しないと。というわけで、手続き型で同じ処理を書いてみました。
const lunchBoxes = [{'唐揚げ': {count: 10}, '玉子焼き': {count: 1}},
{'唐揚げ': {count: 8}},
{'唐揚げ': {count: 6}}];
function eatWithFinger(foodName) {
let canEatIndex = 0;
for (let i = 1; i < lunchBoxes.length; ++i) {
canEatIndex = lunchBoxes[i][foodName].count > lunchBoxes[canEatIndex][foodName].count ? i : canEatIndex;
}
lunchBoxes[canEatIndex][foodName].count--;
}
export default function main() {
for (let i = 0; i < 5; ++i) {
eatWithFinger('唐揚げ');
}
console.log(lunchBoxes);
}
……あれ? さっきの関数型より、この手続き型の方が簡単で分かりやすい?
もう一度、関数型で書いてみた
……冷静になれ、私。
最初のコードをよく見てみると、Ramdaがxだからyしているという部分があって、その結果としてコードが複雑になっています。たとえばR.reduceの引数に初期値が必要とかね。でもこれはRamda的にはしょうがなくて、Ramdaはカリー化を前提にしているので引数の数によるオーバーローディングができないんですよ。だから、R.reduceでは必ず初期値を指定するしかない。
でもね、私が今書いているのはJavaScriptで、JavaScriptでは引数の数によるオーバーローディングは当たり前の技術で、Arrayのreduceは初期値の省略が可能になっています。だから、サクっとreduceの別バージョンを作っちゃいました(Ramdaの公式サイトのサンプルでも、その場で関数をじゃかじゃか追加しているしね)。内容が単純なので、ラムダ式で書きます。
const reduce = (pred, xs) => R.apply(R.reduce(pred), R.juxt([R.head, R.tail])(xs));
あとあれだ、最大の要素を探すときにR.maxByとR.reduceを組み合わせるのも面倒くさかった。なので、別バージョンを。
const maxBy = (pred, xs) => reduce(R.maxBy(pred), xs);
// カリー化を活用してconst maxBy = reduce(R.maxBy(pred))の方が短いけど、引数が消えるとわかりづらくなりそうだったので……。
インデックス化もね。
const indexed = (xs) => R.addIndex(R.map)(R.constructor(Array), xs);
あれ、今作ったmaxByとindexedを組み合わせると、最大の要素のインデックスを取得する関数も作れちゃう?
const maxIndexBy = (pred, xs) => maxBy(R.apply(pred), indexed(xs))[1];
// JavaScriptは引数の数が足りない場合は単純に無視するので、R.apply(pred)するだけで大丈夫。
ついでに、assocPathの値ではなくて関数を取るバージョンを、adjustPathとして定義しちゃいましょう。
const adjustPath = (path, func, xs) => R.assocPath(path, func(R.path(path, xs)), xs);
関数型プログラミングは関数という小さな単位が基本要素なので、組み合わせの際に小回りが利いて実に便利ですな。サクサク新しい関数を作れちゃう。今回作成した関数群は唐揚げ弁当問題に特化していない、汎用的なものなので再利用できそうですしね。
というわけで、これらの関数群をutility.mjsとしてまとめた上で、もう一度関数型プログラミングしてみましょう。
import R from 'ramda';
import {adjustPath, maxIndexBy} from './utility';
const lunchBoxes = [{'唐揚げ': {count: 10}, '玉子焼き': {count: 1}},
{'唐揚げ': {count: 8}},
{'唐揚げ': {count: 6}}];
const canEatIndex = (foodName, lunchBoxes) => maxIndexBy(R.path([foodName, 'count']), lunchBoxes);
const eatWithFinger = (foodName, lunchBoxes) => adjustPath([canEatIndex(foodName, lunchBoxes), foodName, 'count'],
R.dec,
lunchBoxes);
export default function main() {
const eatKaraageWithFingerFiveTimes = R.apply(R.pipe)(R.repeat(R.curry(eatWithFinger)('唐揚げ'), 5));
console.log(eatKaraageWithFingerFiveTimes(lunchBoxes));
}
おお、ちょー短い。canEatIndexは数量が最も大きい食材のインデックスを返すこと、eatWithFingerはその食材の数量をデクリメントすることが、コードからすぐに分かります(adjustPathという関数が何するのかは、R.adjustから推測できるはず……ということにしてください)。
で、上のコードで注目して頂きたい点が、もう一つあります。
今回書き直した際にcanEatIndexを別の関数に分割したわけですけど、手続き型の場合は、このように関数を分割するのはかなり勇気がいります。だって、別にした関数の中でlunchBoxesを変更していないことを確認するには、その関数の中身を確認しなければならないわけですからね。今回みたいに単純なプログラムならいいですけど、でも、大きなプログラムだったり、複数人で開発していたりしたら? 関数型プログラミングは副作用を嫌いますから、関数型プログラミングしていればそんな心配は不要となります(ちなみにeatWithFingerにも副作用はありません。新しいリストを返しますから)。うん、私は関数型プログラミングな人で良かったなぁと。
参考
関数型プログラミングはまず考え方から理解しよう ←元ネタ。
唐揚げつまんでみた ←Haskellやっぱりすげー。Haskell的な書き方をJavaScriptでもやっていてすげー。
PHPでも唐揚げつまんでみた ←PHPでHaskellライクにやってます。すげー。
Ramda ←とても便利。おすすめです。
functional-programming-with-es6-and-ramda ←本稿で作成したコードです。
2017/10/25
Kerasと関数型プログラミングを使えば、深層学習(ディープ・ラーニング)は楽ちんですよ
深層学習(ディープ・ラーニング)ってのは、つまるところ、バックプロパゲーション(逆誤差伝播法)が可能な計算グラフ(計算式)を作って、計算グラフ中のパラメーターに設定すべき値を大量データでキアイで学習させるだけ。しかも、色々と定石が定まってきている(たとえば「畳込みをするならバッチ・ノーマライゼーション→ReLU→畳込みの順にすると精度が上がるよ」とか「分類の場合、畳み込み結果を直接全結合層に入れるより画像全体で平均プーリングした方がパラメーター数が少なくなっていいよ」とか)なので、定石を組み合わせるだけでいろいろできちゃう。ライブラリが計算式をカプセル化してくれますから、計算グラフといっても実際は数式いらずだし。あと、ライブラリが自動でバックプロバゲーション可能な計算グラフを作ってくれるますから、バックプロバゲーションのことも全く考えなくてオッケー。
そして、論文には最新の計算グラフが数式で定義してあるし、大抵はコードも公開されています。だから論文の数式と公開されたコードを読めばすぐに最新の深層学習を適用できる……はずなのですけど、数式は文系の私には読むの大変だし、公開されたコードはなんだか品質が悪くて読みづらい。まぁ、彼らはプログラマーじゃなくて学者さんなのだから、コードにこだわりがないのでしょう。
というわけで、簡単に使えると評判の深層学習ライブラリのKerasと関数型プログラミングを活用して、イマドキの画像認識の計算グラフをできるだけ簡潔なコードで書いてみました。実装したのは、深さより幅というパラダイム・シフトをもたらしたWide ResNetと、少ないパラメーター数で実用的な精度が出て便利なSqueezeNetです。
実装
参考
- Deep Residual Learning for Image Recognition
Wide ResNetの元ネタのResNetの論文です。 - Identity Mappings in Deep Residual Networks
ResNetにどんな修正をすると精度が出るのか、様々な形で実験した論文です。バッチ・ノーマライゼーション→ReLU→畳み込みという定石は、ここかららしい。「試してみた」がいっぱい並んでいるので、学者さんでも結構いきあたりばったりに試していることが分かって楽しい。 - Wide Residual Network
Wide ResNetの論文です。 - SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size
SqueezeNetの論文です。 - 2016年の深層学習を用いた画像認識モデル
論文の解説と、Chainerを使用した様々な論文のニューラル・ネットワークの実装です。Chainer使いの人は、こちらのコードをコピー&ペーストで。 - 画像分類のDeep-CNNを同条件で比較してみる
Chainerを使用して、同じ条件で様々な論文のニューラル・ネットワークの精度を比較しています。Chainer使いの人は、コードが美しいので参考になると思います。
計算グラフの定義は、関数を返す関数を定義する形で
さて、計算グラフの定義と聞くと難しそうなのですけど、実際は、ただの関数の組み合わせでしかありません。add()とsubtract()という関数を使用してx + 1 - 2を表現すると、subtract(add(x, 1), 2)になるというだけ。で、深層学習はこの1や2の部分にどんな値を設定すればよいかを学習するものなので記述は不要ですから、subtract(add(x))みたいなさらに簡単な書き方になります。たとえば、バッチ・ノーマライゼーションしたあとにReLUで活性化して畳み込みをするという定石をKerasで書くと、以下のようになります。
y = Conv2D(...)(Activation('relu')(BatchNormalization()(x)))
なんかおかしな見た目をしているのは、KerasではConv2D(...)と書くと畳み込みをする計算グラフが返されて、それに引数(この場合はx)を渡す形になっているため。関数を返す関数(実際には関数として呼び出せるオブジェクトを返すコンストラクタ)ですな。一般的な言語で言うところの、ラムダ式を返す関数のような感じ。
あれ、ということは、関数合成できちゃう? a(b(c(x)))をf = compose(a, b, c); f(x)と書くアレですよ。Pythonで関数型プログラミングするときに私が使っているライブラリのfuncyにはcompose(数式みたいに右から左に合成)とrcompose(composeの逆順で合成)がありましたので、先ほどのコードを書き換えてみます。今回は、言葉での記述と順序が同じになって分かりやすいrcomposeを使用しました。
y = rcompose(BatchNormalization(),
Activation('relu'),
Conv2D(...))(x)
で、xを渡す(関数を実際に呼び出す)のはモデルを作るときまで遅らせちゃおうと考えれば、バッチ・ノーマライゼーションしてReLUして畳み込みをする計算グラフを返す関数を、以下のように定義できます。
def bn_relu_conv(filters, kernel_size, strides=1):
return rcompose(BatchNormalization(),
Activation('relu'),
Conv2D(filters, kernel_size, strides=strides, ...))
言葉での定義を、ほぼそのまま書いただけ。実にわかりやすいですな。
分岐は、juxtで
でもまぁ、この程度のことはKerasの作者さんは当然ご存知なわけで、だからKerasではSequentialという型が定義されています。Sequentialを使えば、以下のような感じで計算グラフを定義できます。
model = Sequential([BatchNormalization(),
Activation('relu'),
Conv2D(...)])
でもね、この書き方だと分岐と結合が表現できないんですよ。なので、Kerasでは関数型APIというのも提供しています。Kerasのガイドに従ってResNetのresidual unit(下図を参照。畳み込みした結果と、畳込みをしないでショートカットさせたものを足し合わせる)を定義すると、以下のようになります。
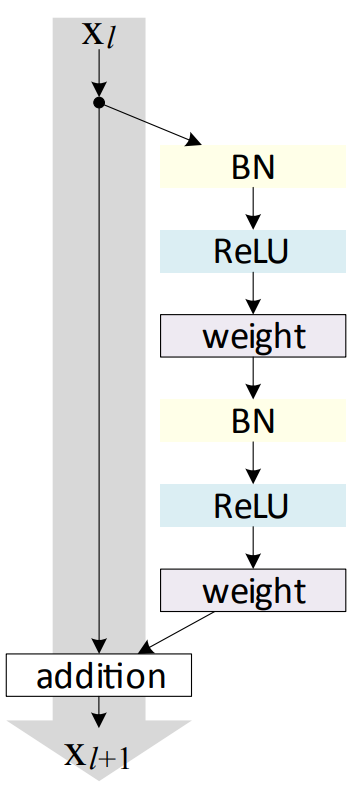
y = BatchNormalization()(x)
y = Activation('relu')(y)
y = Conv2D(64, 3, padding='same', use_bias=False)(y)
y = BatchNormalization()(y)
y = Activation('relu')(y)
y = Conv2D(64, 3, padding='same', use_bias=False)(y)
y = Add()([y, x])
ダメだ、このコードはあまりに醜い……。変数yに何度も再代入するところが特にキモチワルイ。先ほど作成したbn_relu_convを使用して関数化しても……、
def residual_unit(x, filters):
y = rcompose(bn_relu_conv(filters, 3),
bn_relu_conv(filters, 3))(x)
y = Add()([y, x])
return y
やっぱりダメ。関数の種類が2つ(xを引数に取らないで計算グラフを返す関数と、xを引数に取って計算結果を返す関数の2種類)になって、コードを読むときに脳のモードを切り替えなければならなくて、可読性が悪化していますし。
でもね、関数型プログラマーであるfuncyの作者さんは、関数合成ではこのような問題が発生することくらい、もちろんご存知でいらっしゃいます。だから素敵な解決策を用意してくれていて、それがjuxtです。
def inc(x):
return x + 1
def dec(y):
return x - 1
y = juxt(inc, dec)(10) # yは[11, 9]になります。
ただし、funcyはPython3だとジェネレーターを積極的に活用するのにKerasはジェネレーターよりもリストが好きなので、残念ですけどjuxtそのままは使えませんでした。だから、リストを返すljuxtを定義します。そうすれば、residual_unitは以下のように書けます。
def ljuxt(*fs):
return rcompose(juxt(*fs), list)
def residual_unit(filters):
return rcompose(ljuxt(rcompose(bn_relu_conv(filters, 3),
bn_relu_conv(filters, 3)),
identity),
Add())
なお、上のコードで使用しているidentityってのは引数をそのまま返す関数で、これを使えばf(x) + xをrcompose(juxt(f, identity), operator.add)で表現できるわけですね。
これで、関数の種類が1つだけになって、変数の再代入がなくなって細かい変数名を突合しなくても分岐と結合があることが明確になって、うん、可読性が上がってコードが美しい!
Wide ResNet
以上で書き方が決まりましたので、Wide ResNetを実装してみました。計算グラフを定義する部分のコードを以下に載せます。
def computational_graph(class_size):
# Utility functions.
def ljuxt(*fs):
return rcompose(juxt(*fs), list)
def batch_normalization():
return BatchNormalization()
def relu():
return Activation('relu')
def conv(filter_size, kernel_size, stride_size=1):
return Conv2D(filter_size, kernel_size, strides=stride_size, padding='same',
kernel_initializer='he_normal', kernel_regularizer=l2(0.0005), use_bias=False)
# ReLUしたいならウェイトをHe初期化するのが基本らしい。
# Kerasにはweight decayがないので、kernel_regularizerで代替しました。
def add():
return Add()
def global_average_pooling():
return GlobalAveragePooling2D()
def dense(unit_size, activation):
return Dense(unit_size, activation=activation, kernel_regularizer=l2(0.0005))
# Kerasにはweight decayがないので、kernel_regularizerで代替しました。
# Define WRN-28-10
def first_residual_unit(filter_size, stride_size):
return rcompose(batch_normalization(),
relu(),
ljuxt(rcompose(conv(filter_size, 3, stride_size),
batch_normalization(),
relu(),
conv(filter_size, 3, 1)),
rcompose(conv(filter_size, 1, stride_size))),
add())
def residual_unit(filter_size):
return rcompose(ljuxt(rcompose(batch_normalization(),
relu(),
conv(filter_size, 3),
batch_normalization(),
relu(),
conv(filter_size, 3)),
identity),
add())
def residual_block(filter_size, stride_size, unit_size):
return rcompose(first_residual_unit(filter_size, stride_size),
rcompose(*repeatedly(partial(residual_unit, filter_size), unit_size - 1)))
k = 10 # 論文によれば、CIFAR-10に最適な値は10。
n = 4 # 論文によれば、CIFAR-10に最適な値は4。
# WRN-28なのに4になっているのは、28はdepthで、depthはconvの数で、1(最初のconv)+ 3 * n * 2 + 3(ショートカットのconv?)だからみたい。
return rcompose(conv(16, 3),
residual_block(16 * k, 1, n),
residual_block(32 * k, 2, n),
residual_block(64 * k, 2, n),
batch_normalization(),
relu(),
global_average_pooling(),
dense(class_size, 'softmax'))
うん、簡単ですな。どんな計算グラフなのかが、コードからすぐに読み取れます。なお、上のコードでバッチ・ノーマライゼーション→ReLU→畳み込みを関数にまとめていないのは、Deep Pyramidal Redisual Networksの3.3.1に書いてあるように、residual blockの最初のReLUを削って最後にバッチ・ノーマライゼーションを追加するとさらに精度が向上するらしいから。今後もこういう細かい変化が出てくると思うんですよね。
ちなみに、Wide ResNetはこんな感じの計算グラフです(Wide ResNetの元ネタのResNet論文の画像なので、少し異なりますけど)。

SqueezeNet
SqueezeNetは、こんな感じ。
def computational_graph(class_size):
# Utility functions.
def ljuxt(*fs):
return rcompose(juxt(*fs), list)
def batch_normalization():
return BatchNormalization()
def relu():
return Activation('relu')
def conv(filters, kernel_size):
return Conv2D(filters, kernel_size, padding='same', kernel_initializer='he_normal', kernel_regularizer=l2(0.0001))
def concatenate():
return Concatenate()
def add():
return Add()
def max_pooling():
return MaxPooling2D()
def dropout():
return Dropout(0.5)
def global_average_pooling():
return GlobalAveragePooling2D()
def softmax():
return Activation('softmax')
# Define SqueezeNet.
def fire_module(filters_squeeze, filters_expand):
return rcompose(batch_normalization(),
relu(),
conv(filters_squeeze, 1),
batch_normalization(),
relu(),
ljuxt(conv(filters_expand // 2, 1),
conv(filters_expand // 2, 3)),
concatenate())
def fire_module_with_shortcut(filters_squeeze, filters_expand):
return rcompose(ljuxt(fire_module(filters_squeeze, filters_expand),
identity),
add())
return rcompose(conv(96, 3),
max_pooling(),
fire_module(16, 128),
fire_module_with_shortcut(16, 128),
fire_module(32, 256),
max_pooling(),
fire_module_with_shortcut(32, 256),
fire_module(48, 384),
fire_module_with_shortcut(48, 384),
fire_module(64, 512),
max_pooling(),
fire_module_with_shortcut(64, 512),
batch_normalization(),
relu(),
conv(class_size, 1),
global_average_pooling(),
softmax())
ちなみに、SqueezeNetはこんな感じの計算グラフです。
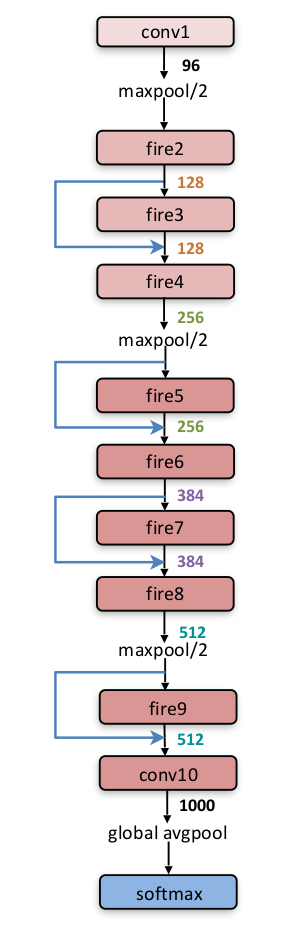
fireと書かれている部分の構造は以下のような感じ。
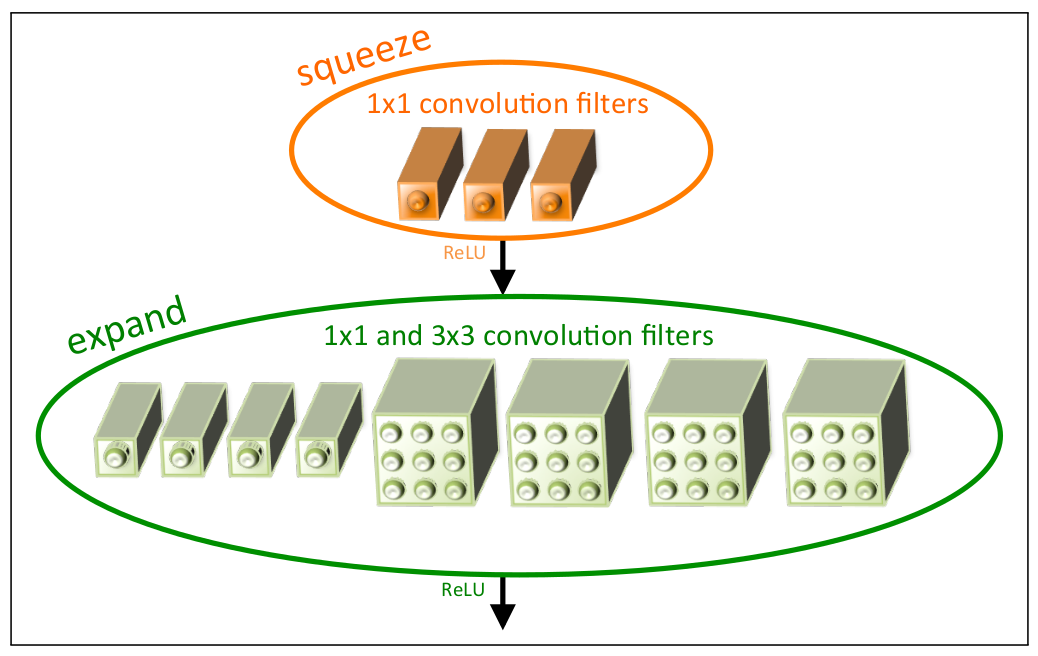
えっと、論文だとSqueezeNetは浮動小数点のビット数を減らしても精度が下がらないと書かれていてスゴそうだったのですけど、浮動小数点の精度を下げる方法が分からなかったので試していません。中途半端でごめんなさい……。
なにはともあれ
関数型プログラミング最高! Kerasとfuncyとnutszebraさんとtakedartsさんありがとー!