文系の、文系による、文系のためのTensorFlow入門 #1
2016/04/25
- 本稿は「ニューラルネットワークと深層学習」を参考にして作成しています。とても優れた無料のオンライン書籍ですので、ぜひご一読ください。
- 本稿はディープ・ラーニングの素人が書いています。だからあまり信用すんな! あと、お願い誰かチェックして……。
- 遠回りしまくりで、なかなかTensorFlowに入りません。覚悟してください。
- 使用する言語は、Python3.5.1です。Python2.7より、かなり良いですよ。
人工ニューロン
脳はニューロンで構成されているわけで、だったらそのニューロン相当品を作ってつなげてやれば、脳相当品を作れるんじゃね? というわけで考え出されたのが、以下に図示すパーセプトロンです。

パーセプトロンは、コンピューター資源が限られていた1958年に発表されただけあってとても単純です。左側に出ている線が入力で、右側の線が出力。入力も出力も、0か1の2値しかとりません。入力に重みを掛けて足し合わせた結果が閾値を超えたら出力は1に、そうでなければ出力は0になります。
具体例を挙げましょう。朝起きて、会社に行って働くか、それとも休んでで家でダラダラするかを決断するパーセプトロンを作成してみます。入力は、有給休暇が残っているか(残っていれば1)、体調が良いか(良ければ1)、やらなければならない仕事があるか(あれば1)とします。私の魂の声に忠実にこのパーセプトロン相当品をプログラミングすると、以下のコードになります。
def goes_to_office(has_holidays, good_condition, has_work):
return has_holidays * -3 + good_condition * 1 + has_work * 1 > -1
有給があれば(has_holidaysが1なら)休む、有給がなくなったらしょうがないので会社に行くというロジックですね(私の魂の声は、good_conditionとhas_workは無視しちゃうみたいです)。でも、これだとさすがに社会人失格ですから、自分を曲げて、まだ有給が残っていても、体調が良くて仕事があるなら会社に行かないとね。
def goes_to_office(has_holidays, good_condition, has_work):
return has_holidays * -3 + good_condition * 1 + has_work * 1 > -2
はい、パラメーターをちょっと変えただけで実現できました。人工ニューロン、なかなかやるじゃん。
フィードフォワード・ニューラル・ネットワーク
とはいえ、人工ニューロン1つだけではできることに限りがありますから、いっぱい繋げてみましょう。単純化のために、いくつか層を作成して、データは一方向にしか流れないものとします。ある層の人工ニューロンの出力が、次の層の人工ニューロンの入力になるわけ。あと、ある層と次の層のニューロンは、全部繋げちゃいます。図にすると、以下のような感じ。
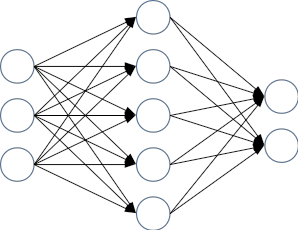
このようなニューラル・ネットワークで、0~9の手書きの数字を処理することを考えてみます。たとえばものすごく几帳面な人が書いた手書きの数字の0をスキャナーで読み込むと、以下のようになるでしょう。
□□□□□□□□
□□■■■■□□
□■□□□□■□
□■□□□□■□
□■□□□□■□
□■□□□□■□
□□■■■■□□
□□□□□□□□
白い四角を0、黒い四角を1とすれば、上の例なら8×8で64個の数値で表現できます。これらの数値が64個の入力となって、ニューラル・ネットワークに入ってくるわけです。これらの入力を処理する人工ニューロンの重みづけと閾値次第では、例えば以下に示す画像の黒い四角の部分が1の場合に1を出力するようにできるでしょう(白い四角の部分は、先ほどの体調の良し悪しや仕事の有無のように、出力には影響しないように重みづけと閾値を調節しておきます)。
□□□□□□□□
□□■■□□□□
□■□□□□□□
□■□□□□□□
□□□□□□□□
□□□□□□□□
□□□□□□□□
□□□□□□□□
同様に、0の右上部分や、左下部分、右下部分に対して1を出力する人工ニューロンも作れます。
それだけではありません。人工ニューロンがいっぱいあるなら、以下に示すような歪んだ0の一部分に反応する人工ニューロンも作れるでしょう(きれいな0の一部でも歪んだ0の一部でも反応する人工ニューロンでも良いです)。
□□□□□□□□
□□□■■■□□
□□■□□□■□
□■□□□□■□
□■□□□□■□
□□■□□■□□
□□□■■■□□
□□□□□□□□
そして、次の層に、これらの人工ニューロンが1を出力した場合に1を出力する人工ニューロンがあるとしたら? もしその人工ニューロンが1を出力したなら、入力された手書きの数字は0だと言えるでしょう。8を0と間違えないよう、中央にある横棒に反応する人工ニューロンが1を出力した場合は1を出力しないように重みづけと閾値が設定されていれば、もう完璧です。
というわけで、手書き文字の認識という高度な処理を、やたらと単純な人工ニューロンの積み重ねで実現できちゃいました!
活性化関数
じゃあ数字の0~9の一部分をうまいこと判定する人工ニューロンの重みづけと閾値を手で書いてやるぜぇ……というのは、まぁ、無理ですよね。だから、なんとかして重みづけと閾値を機械学習させたい。
その際に問題になるのは、重みづけや閾値と出力の関係がぶった切れているといううことです。だって、出力は0か1の2値なんですから。ある日突然離婚を切り出されたのでは、どこがどう悪かったのか分からないような感じです。
でも、もし出力が0.836のような実数なら、重みづけや閾値を少し変更すると出力も少し変更するという感じにできるわけです。休日に一人で遊びに出かけたら配偶者が少し不機嫌になったので、次からは平日に会社を休んで遊びに行こうって感じ。ほら、少しずつ調整できたでしょ?
というわけで、人工ニューロンへの入力も出力も実数としましょう。そのために、人工ニューロンの出力を「重みづけした入力の合計が閾値を超えたら1」から、「重みづけした入力の合計にバイアスを足した数」にします。以下のような感じ。
def goes_to_office(has_holidays, good_condition, has_work):
return -3.0 * has_holidays + 1.0 * good_condition + 1.0 * has_work + 2.0 # 「> -2」を「+ 2.0」に変更しました。
でも、まだこれだけでは不十分なのだそうです。というのも、人工ニューロンの出力の変化が一定(線形)だと、ニューラル・ネットワークは単純な処理しかできないらしいんですよ。なので、グラフを描いたときに直線にならない(非線形な)結果になるような関数を用意してあげなければなりません。このような関数を、活性化関数と呼びます。
で、私ではイマイチ違いが分からなかったのですけど、活性化関数はいくつも種類があるみたい。伝統的なのはシグモイド関数で、今流行しているのはReLUというやつらしい。どちらの関数もTensorFlowが提供しているので、実装そのものは呼び出すだけと簡単です。ReLUを使えば間違いはないけど、上手くいかないときはTensorFlowの活性化関数群から適当に選んで入れ替えてみなさいって死んだばっちゃんが言っていました(理屈が分かる人は、理屈に合わせて入れ替えてください)。
ここまでを、TensorFlowでプログラミングしてみる
なんだ、ニューラル・ネットワークって別に難しくないじゃん。多数の小人さんが連なって伝言ゲームをしているような感じですな。さっそく作ってみよう……と思うのですけれど、人工ニューロンがいっぱいあって、重みづけもバイアスも多数あって、そんなのを一つづつ変数や関数として書くなんてのは大変すぎます。だから、行列を使って楽をすることにしましょう。
さて、私が行列について知っていることは、行列の掛け算をするときには積ABが定義されるのはAの列の本数とBの行の本数が一致している場合に限られるのと、掛け算の結果はAの行とBの列の行列になるってことだけ。
これを先ほどの人工ニューロンの話に適用すると、たとえば1行64列の画像の行列と64行10列の重みづけの行列は掛け算が可能で、その結果は1行10列の行列になるということになります(しかも、掛け算では数値を掛け算した結果を足し算するという、人工ニューロンのところで書いたプログラムと同じ計算がなされます)。画像を一枚入力に渡せば10個の数値になるわけですから、これはある層全体の重みづけ部分の計算そのものです。バイアスを足す部分は、その結果に1行10列の重みづけの行列を足し算すればOK。というわけで、ニューラル・ネットワークの1層分(コードを簡略化するために、入力は5個でニューロンの数は3とします)をPythonの数値演算ライブラリのNumPy(TensorFlowはもう少しだけ待って)で表現すると、以下のコードになります。
```python import numpy as np
データ作成。
x = np.matrix([0.01, 0.02, 0.03, 0.04, 0.05]) # 入力。1行5列。値は適当。 w = np.matrix([[0.06, 0.07, 0.08] # 重みづけ。5行3列。値は適当。 [0.09, 0.10, 0.11] [0.12, 0.13, 0.14] [0.15, 0.16, 0.17] [0.18, 0.19, 0.20]]) b = np.matrix([0.21, 0.22, 0.23]) # バイアス。1行3列。値は適当。
ネットワークの定義。
layer_1_out = x * w + b # 1行3列の出力になる。活性化関数は未使用。
あらまぁ、とっても簡単……。でも、TensorFlowだと、もう少し難しくなります。というのも、TensorFlowではどのような計算をするかの定義と、定義した計算の実行を分けて記述しなければならないんですよ。こんな面倒な方式になっているのは、学習をさせるにはどのような計算をしたのかという情報が必要になるため(Chainerというディープ・ラーニングのライブラリでは、コード上での定義と実行が一つになっていますけど、実行時に裏で計算グラフを作っています)。
というわけで、TensorFlowの流儀に従うことにしましょう。まずはニューラル・ネットワークの定義えす。題材は、28ドット×28ドットの0~9の手書き数字を認識する、MNISTとします。
~~~ python
# ニューラル・ネットワークの構築はinferenceでやれとチュートリアルに書いてあった。
def inference(l0): # l0は、ニューラル・ネットワークへの入力となる行列。今回は、28ドット×28ドットの画像データを1行784列の行列にしたもの。
# name_scope()しておくと、後述するTensorBoardでの表示がわかりやすくになります。なお、入力でも出力でもない層を、隠れ層と呼びます。
with tf.name_scope('hidden'): # 「隠れ」層なので名前はhidden。
# Variable型の、重み付けの行列を作成します。truncated_normalにすると、いい感じに分布する乱数で初期化されるらしい。
# 引数が、行列の次元です。入力が784列なので、最初の値は784に決まります。次の値を100にして、隠れ層のニューロンの数を100にしました。
# なお、戻り値のw1は計算式そのものなので、printしても値はわかりません(Chainerだと、printできてデバッグが楽らしい)。
w1 = tf.Variable(tf.truncated_normal([784, 100]))
# Variable型の、バイアスの行列を作成します。constantは定数での初期化。
# TensorFlowのチュートリアルでは0.1に初期化したのが多かったので、何も考えずに0.1で初期化しました。ただの初期値だしね。
# shapeが行列の次元。ニューロンの数を100にしたので、100になります。
b1 = tf.Variable(tf.constant(0.1, shape=[100]))
# 入力に重みを掛け算して、バイアスを足して、活性化関数に通します。
# 活性化関数は、ReLUを使用しました。ReLUの数式の意味はわかりませんでしたけど、APIを呼び出すだけなので簡単でした。
l1 = tf.nn.relu(tf.add(tf.matmul(l0, w1), b1))
# 出力層。0〜9のそれぞれに反応するニューロンが欲しいので、ニューロンの数は10個にします。
with tf.name_scope('output'):
w2 = tf.Variable(tf.truncated_normal([100, 10]))
b2 = tf.Variable(tf.constant(0.1, shape=[10]))
l2 = tf.add(tf.matmul(l1, w2), b2) # 出力の使い方を制限させないために、あえて活性化関数は入れていません。
# 計算結果(を表現する計算グラフ)を返します。
return l2
APIを調べるのは少し面倒でしたけど、コードそのものはかなり簡単でした。
損失関数
先ほど作成したニューラル・ネットワークは、まだ何も学習していないのでヘコヘコです。だから学習をさせたいのですけれど、そのためにはどのようにニューラル・ネットワークを修正していけば良いのかを表現する「損失関数」ってのが必要になります。しかも、この損失関数は、出力層の方から少しずつ修正を伝播させていくバックプロパゲーションという学習のためのアルゴリズムとの相性があるらしい。
この損失関数にはやっぱりいくつかあって、クロス・エントロピーってのが有名みたいです。で、Webを見ていくとクロス・エントロピーの数式が載っているのですけど、まぁこれが全くワカラナイ。だから、TensorFlowのAPIに丸投げしました。
# 損失関数はloss()でやれと、チュートリアルに書いてあった。
def loss(logits, labels):
# 引数のlogitsはニューラル・ネットワークの出力、labelsは正解データ。
# labelsと複数形になっているのは、後述するバッチ単位で損失関数を実行するため。
# nn.sparse_softmax_cross_entropy_with_logitsは、どれか一つのニューロンを選ぶ(0と1の両方はありえない)場合用の関数。
# reduce_meanでその平均を計算しているのは、これもやっぱり後述するバッチ単位で損失関数は実行されるため。
# tf.castしているのは、正解データはint32だけど関数がint64じゃないと嫌だとわがままを言ったため。
return with_scalar_summary(
tf.reduce_mean(tf.nn.sparse_softmax_cross_entropy_with_logits(logits, tf.cast(labels, tf.int64)), name='loss'))
# 値を、後述するTensorBoard向けに出力させる関数。
# ここまでのコードは計算方法を定義しているだけで、logitsやlabelsなどの変数は計算をすると値が設定される「場所」を指しているに過ぎません。
# なので、printとかしても全く無駄です。だから、xxx_summaryしてTensorBoardで見ます。
# 損失関数は学習がうまく行っているかどうかの判断にとても役立つので、作成したwith_scalar_summaryを通して出力対象に設定しておきます。
def with_scalar_summary(op):
tf.scalar_summary(op.name, op)
return op
TensorFlowなら、数式いらずですな。
最適化
さて、作成した損失関数を活用してバックプロバゲーションして学習するわけですけど、ゴール目指していい感じに最適化するアルゴリズムとして最急降下法ってのがあります(詳細は私以外の人に聞いてください……)。TensorFlowは、このアルゴリズムをtrain.GradientDescentOptimizerで提供しています。TensorFlowは他にもいろいろな最適化アルゴリズムがあって、train.AdamOptimizerってのが良いらしい(学習レートを自動で調整してくれる)。でも、今回は学習レートが学習に与える影響を調べたかったので、最も基本的なtrain.GradientDescentOptimizerを使用してみました。
# 最適化方法はtrainingで示せと、チュートリアルに書いてあった。
def training(loss, learning_rate):
# 引数のlossは、損失関数。learning_rateは学習レートと呼ばれるもの。
# 学習レート変えるとうまく学習するようになるというか、調整して適切な値に設定しないと全然学習されなくて涙が出る。
# minimizeは最小化するように頑張れという指示。
return tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
さて、ディープ・ラーニングというと必ず出てくるバックプロパゲーションですが、私は全く理解していません。というのも、TensorFlowが自動でやってくれるんですよね。だから、ここまでに作成したコードだけで、バックプロパゲーションでニューラル・ネットワークの学習が可能です。
評価関数
でも、損失関数の値が0.23になった……とか言われても、それがどの程度凄いのかは全くわかりませんので、正解数などの指標を提供する関数も作っておきましょう。TensorFlowは、正解不正解を確認するためのAPIも用意してくれています。nn.in_top_kを使うと、今回のlogitsの出力である10個の数値のうち、値が大きい上位k個のインデックスのどれかがlabelと一致すればTrueになります。今回はkに1を入れて、正解かどうかを判断しました(「この写真に表示されているのは犬か猫か車のどれかだと思う」と出力するシステムの場合は、kを3にしてください)。
# 評価をする計算グラフはevaluationで作れと、チュートリアルに書いてあった。
def evaluation(logits, labels):
# TrueやFalseだと計算できないのでint32にキャストして、reduce_sumで合計します。Trueは1、Falseは0になります。
return with_scalar_summary(tf.reduce_sum(tf.cast(tf.nn.in_top_k(logits, labels, 1), tf.int32), name='evaluation'))
もう、いたれりつくせりですな。
データを読み込んで学習させる
これで、ディープ・ラーニング関連の話は完了! あとは普通に学習させるだけ。
学習で重要なのは、バッチと呼ばれる複数データ単位で学習させることです。1回処理するたびにニューラル・ネットワークを調整すると、学習が迷走しちゃうんですよ。細かい単位で学習するのは、ダイエットで日々の体重の変化に一喜一憂して、たとえば今日は昨日より体重が1kg減ったから、昨日と同じメニューにすれば明日は更に1kg減ると考えるようなものです(朝トイレで超大物を産んだことが、1kg体重が減った原因だと思うよ)。
あと、教育用のデータとは別に、評価用のデータを用意することも重要です。コンピューターは融通が効かないので、教育用のデータに含まれる一般的ではない癖を学習しちゃったりします。教科書を丸暗記してどのページでも暗唱できるようになったけど、少し言い回しが変わっただけで答えられないというような感じ。このような状況を過学習と呼び、過学習を防ぐためのテクニックもあるのですけど、面倒なので今回は大量のデータで回避します。
学習部分の実装は、コード量は少し多いけれど簡単です。MNISTのデータをダウンロードして行列化する処理はTensorFlowのサンプルにあった(tensorflow.examples.tutorials.mnist.input_data)ので、それをそのまま使用します。入力と正解を関数グラフに渡すための入れ物はplaceholderで作成できます。あとは、計算グラフを実行する環境であるSessionを作成して、Sessionのrunメソッドを呼ぶだけ。学習した結果が見えないとさみしいので、TensorBoardと画面に出力する処理も少しだけ作りましょう。
# TensorFlowのサンプルを使用して、MNISTのデータを読み込みます。
from tensorflow.examples.tutorials.mnist import input_data
data_sets = input_data.read_data_sets('MNIST_data/')
# 入力と正解の入れ物を作成します。次元の最初の数値がNoneになっているのは、バッチやテスト用データのサイズに合わせたいから。
inputs = tf.placeholder(tf.float32, [None, 784], name='inputs')
labels = tf.placeholder(tf.int32, [None], name='labels')
# これまでに作成した関数を使用して、計算グラフを作成します。
logits = inference(inputs)
loss = loss(logits, labels)
training = training(loss, 1.0) # 学習レートは、試した範囲では1.0が一番良かったです。
evaluation = evaluation(logits, labels)
# tensorboardへの出力のための計算グラフを作成します。
summary = tf.merge_all_summaries()
# 作成した計算グラフの実行は、Sessionを通じて実施します。
with tf.Session() as session:
# 変数を初期化する計算グラフを実行します。session.run(計算グラフ)で、実行できます。
session.run(tf.initialize_all_variables())
# tensorboardへの出力ライブラリ。
summary_writer = tf.train.SummaryWriter('MNIST_train/', session.graph)
# バッチを1万回実行します。本当は、いい感じに学習できたら終了にすべきなのですけど……。
for i in range(10000):
# TensorFlowのサンプルのMNIST読み込みライブラリは、next_batch(件数)で、指定された件数のデータを読み込みます。
# 今回は、100件単位で学習することにしました。
batch = data_sets.train.next_batch(100)
# placeholderへのデータの設定は、ディクショナリを使用して実現されます。
feed_dict = {inputs: batch[0], labels: batch[1]}
# 学習して、損失関数の値を取得します。学習の結果は捨てて、損失関数の値だけを変数に代入します。
_, loss_value = session.run([training, loss], feed_dict=feed_dict)
# 時々は、TensorBoardや画面にデータを出力します。
if i % 100 == 0 and i != 0:
# TensorBoardにデータを出力しhます。
summary_writer.add_summary(session.run(summary, feed_dict=feed_dict), i)
summary_writer.flush()
# 損失関数の値を画面に出力します。
print('Step %4d: loss = %.2f' % (i, loss_value))
# 訓練用データとは別のテスト用データで評価して、結果を画面に出力します。
evaluation_value = session.run(evaluation,
feed_dict={inputs: data_sets.test.images,
labels: data_sets.test.labels})
print('Score = %d/%d, precision = %.04f' %
(evaluation_value, data_sets.test.num_examples, evaluation_value / data_sets.test.num_examples))
試してみる
作成したプログラムを実行してみたら、正答率は94.1%になりました! TensorFlowのチュートリアルの「MNIST For ML Beginners」での正答率は92%くらい、「Deep MNIST for Experts」の正答率は99.2%くらいらしいので、これで、初心者に毛が生えた程度にはなれました。
TensorBoard
TensorBoardの画面も載せておきます。グラフを見ると値があまり安定していないので、チューニング不足なのかもしれません。
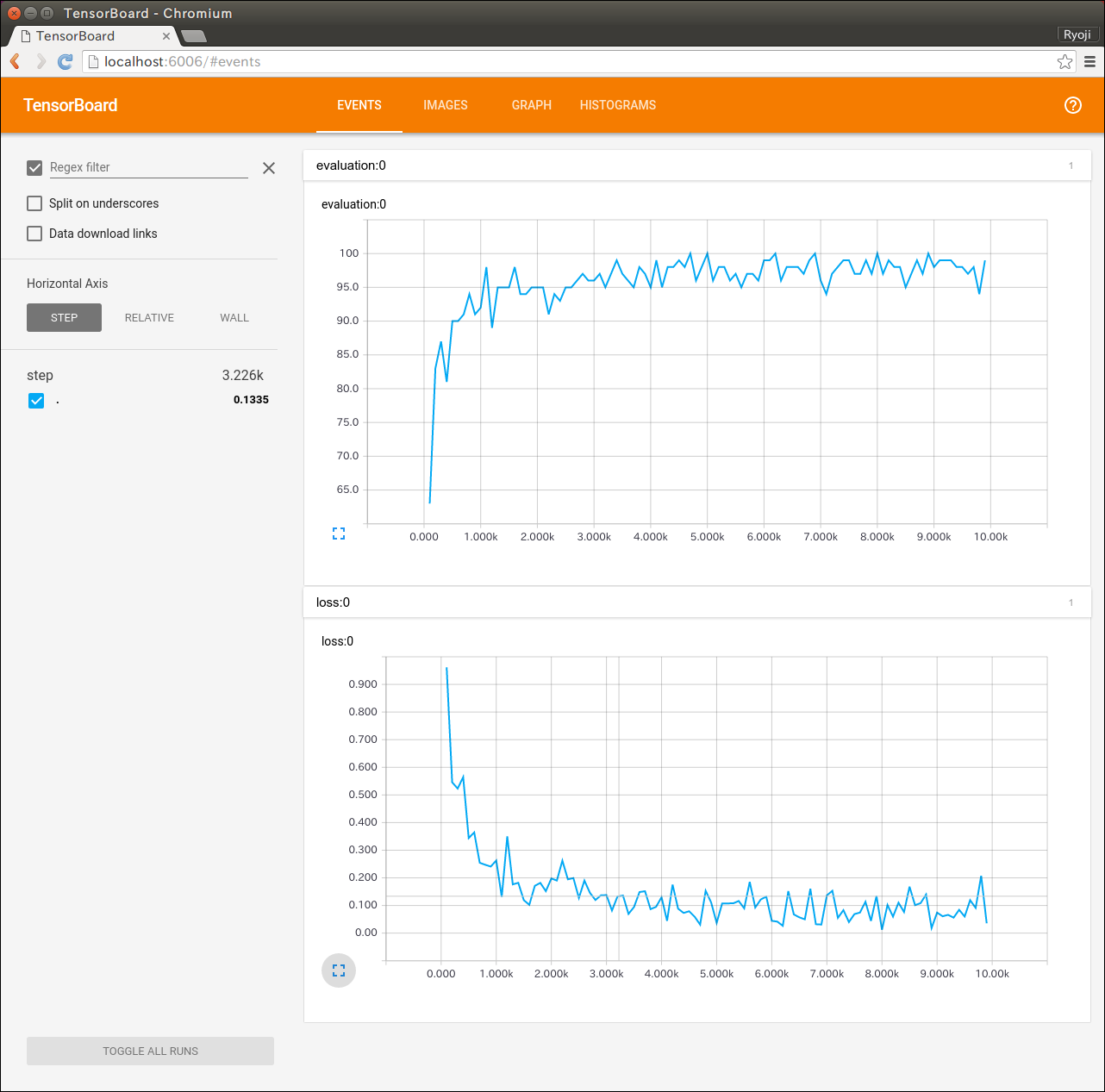
TensorBoardでは計算グラフも可視化できます。計算式を図示するので大きな図になって、すごいことをやっているみたいに勘違いできてちょっと楽しい。
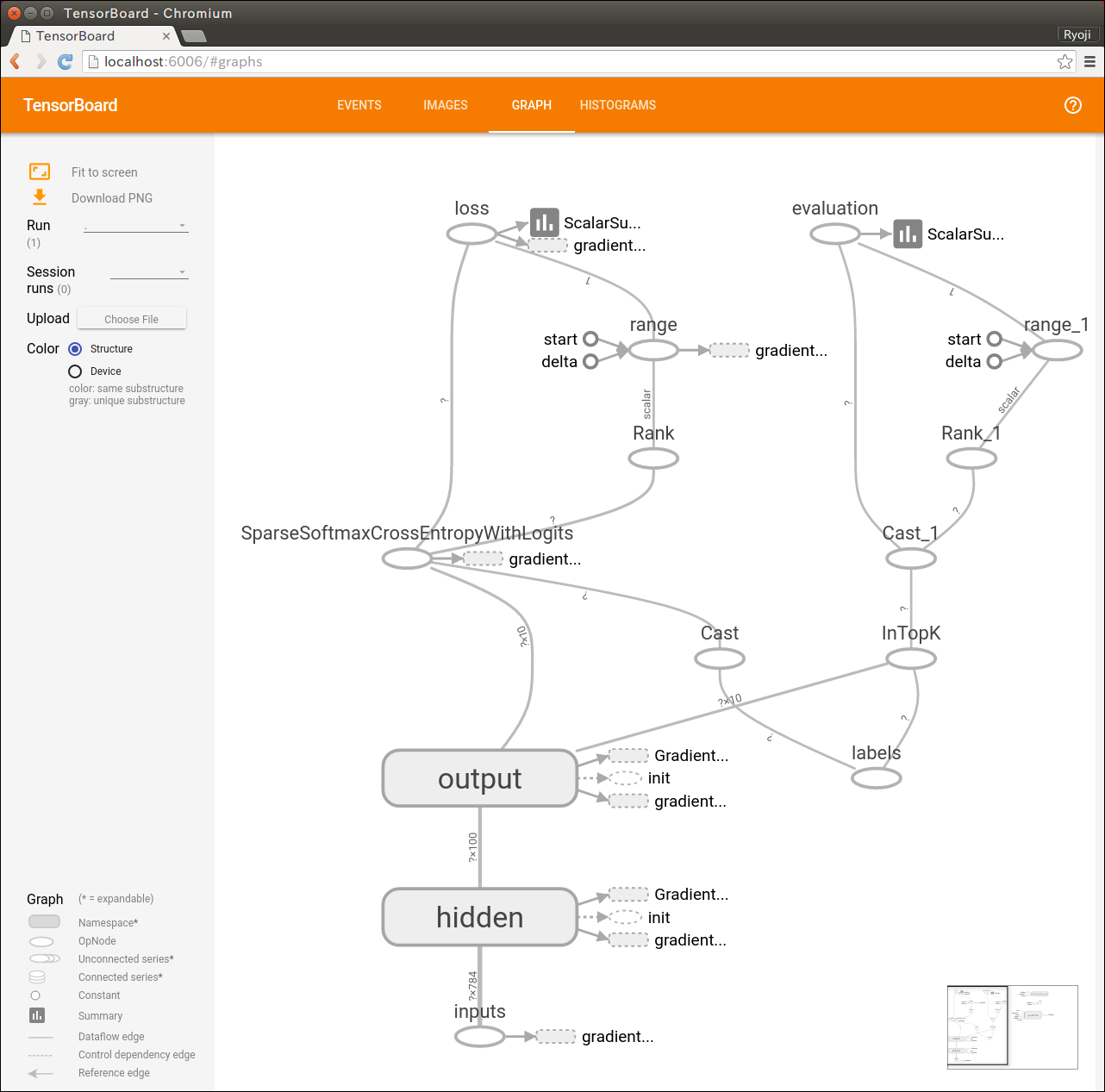
ニューラル・ネットワークは、左下の小さな部分だけなんだけどね。
次は?
まずは効果絶大との噂の畳み込みニューラル・ネットワーク。で、過学習を防ぐための正則化。それが終わったら、層単位で教師なし学習させるオート・エンコーダーあたりを。学習結果を保存してサービス化する方法もやらないと……。