浮動小数点の誤差にご用心！

2017/04/27

ゲームを作っていたら（←SIerで働いているとは思えない書き出し）、浮動小数点の誤差でひどい目にあいました……。同じ穴にハマる方がいらっしゃるかもしれないので、注意喚起を。

そのゲームはキャラクターが重なってはならない仕様だったので、移動する2つの球の衝突判定を使いました。移動する2つの球の衝突判定は2次方程式を解く形になっているので、以下のような関数になります。

def solve_quadratic_equation(a, b, c):
    d = b ** 2 - 4 * a * c

    if d >= 0:
        return ((-b + math.sqrt(d)) / (2 * a),
                (-b - math.sqrt(d)) / (2 * a))

    return ()

昔学校で習ってその後完全に忘れた、「まいなすびーぷらすまいまするーとびーにじょうまいなすよんえーしーわるにえー」って奴ですな。で、この関数を使って衝突判定してみたところ、なんだか時々おかしな動作をします。具体的には、キャラクターが少しだけ食い込んじゃう時がある（キャラクターが重なった状態でもう一度衝突判定すると、キャラクターが離れる瞬間を衝突と間違えて堂々巡りするというバグになっちゃう）。

これは多分浮動小数点の誤差でしょうとあたりをつけてインターネットを検索してみたら、どうやら、2次方程式の解の公式をそのままプログラミングするのは素人らしい。30年以上プログラムを組んでいるのに、いまだ素人でしたか、私は……。

なんでも、同じ値の浮動小数点の引き算は精度が落ちるので、-b +/- math.sqrt(d)の部分がダメなんだって。math.sqrt()の結果は正の数なので、bがどんな値であっても必ず引き算が発生しちゃうというわけ。ではどうするかというと、2次方程式の解の係数の関係を使うんだそうです。2次方程式は2乗しているので解が2つあるわけで、それをαとβとした場合、α + β == -b / aとα * β == c / aという関係が成り立つんだって。だから、引き算がない方を使ってとりあえず解を一つ見つけて、解の係数の関係を使ってもう一つの解を求めればよい。コードにすると、こんな感じ。

def solve_quadratic_equation(a, b, c):
    d = b ** 2 - 4 * a * c

    if d >= 0:
        if b >= 0:
            x = (-b - math.sqrt(d)) / (2 * a)
        else:
            x = (-b + math.sqrt(d)) / (2 * a)

        return (x, c / a / x) if x != 0 else (x, x)

    return ()

さて、このコードの効果は？　誤差がどのくらい減るのか、可視化してみましょう。-b + math.sqrt(b ** 2 - 4 * a * c)が問題なのだから、bの絶対値が大きくてaとcが小さい場合に誤差がでるはず。だからbの値は大きくしたい。あと、正解を簡単に計算できるようにもしておきたい。というわけで、aとcを1に固定して、x ** 2 - (10 ** n + 10 ** -n) * x + 1の場合でやりましょう。この場合の正解は10 ** nと10 ** -nになるはず。あとは誤差を計算してグラフを描くだけ。というわけで、可視化のコードは以下の通り。

import math
import matplotlib.pyplot as plot
import numpy as np

from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D


def solve_quadratic_equation_1(a, b, c):
    d = b ** 2 - 4 * a * c

    if d >= 0:
        return ((-b + math.sqrt(d)) / (2 * a),
                (-b - math.sqrt(d)) / (2 * a))

    return ()


def solve_quadratic_equation_2(a, b, c):
    d = b ** 2 - 4 * a * c

    if d >= 0:
        if b >= 0:
            x = (-b - math.sqrt(d)) / (2 * a)
        else:
            x = (-b + math.sqrt(d)) / (2 * a)

        return (x, c / a / x) if x != 0 else (x, x)

    return ()


def visualize(f):
    def error(n):
        a,  b  = sorted((10 ** n, 10 ** -n))
        a_, b_ = sorted(f(1, -(10 ** n + 10 ** -n), 1))

        return (n, max(math.fabs(a - a_), math.fabs(b - b_)))

    def errors():
        return tuple(map(error, np.linspace(0, 10, 100)))

    x, y = zip(*errors())

    plot.plot(x, y)
    plot.show()


if __name__ == '__main__':
    visualize(solve_quadratic_equation_1)
    visualize(solve_quadratic_equation_2)

可視化結果は、こんな感じ。

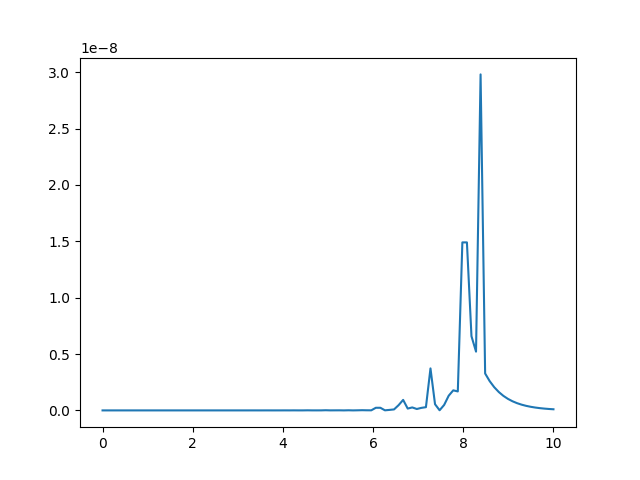
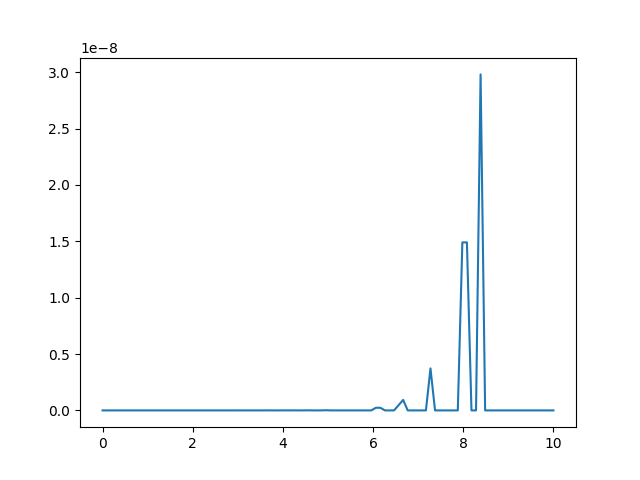
……確かに誤差が出るケースは少なくなったけど、大きな誤差がでる場合の、誤差の量そのものは変わらないじゃん！　というわけで、このコードでもやっぱり誤差は出ちゃいます。だから、今回は、誤差の許容量であるEPSを変えて対応しました。今回私がハマった穴というのは、浮動小数点と二次方程式じゃなくて、可視化してみないと効果はわからないという部分です。皆様気をつけて！　やっぱり、可視化は大事ですよ。

そもそも、どうして私は浮動小数点の誤差を押さえ込めると考えちゃったんだろ？

if float(2 ** 53) == float(2 ** 53) + 1:
    print('xとx+1は等しい')

だって、上のコードを実行すると「xとx+1は等しい」と表示されちゃうくらい、浮動小数点は不完全なのに……。

追記

ごめんなさい。可視化プログラムにバグがありました。上のコードの-(10 ** n + 10 ** -n)では、nが大きくなると、本文の最後に挙げた大きな数値に小さな数値を足しても結果が変わらないのと同じ浮動小数点の誤差が発生します。具体的にはグラフの右の端、8を超えたあたりからは、この誤差によって意味がないグラフになっています。だから、ごめんなさい、グラフの右端は見ないようにしてください。

あと、コード・レビューしてくれた親切な人が教えてくれた、バグがあるのに正しい答えが出ちゃっているように見える理由も。上のコードのsolve_quadratic_equation_2()のd = b ** 2 - 4 * a * cのところ、b ** 2に比べて4 * a * cがとても小さい場合は-b - math.sqrt(b ** 2) / (2 * a)と同じコードになり、aは1なので-b - b / 2になって、だから、正しい答えの一つが手に入っちゃうというわけ。情けないことに、レビューしてもらうまで全く気がついていませんでした。

結論は、可視化だけでは不十分、コード・レビューも必要ということですね……。